Alpha-beta Pruning in Artificial Intelligence

In the realm of artificial intelligence (AI), particularly in game-playing scenarios, decision-making efficiency is paramount. Among the various techniques employed to enhance performance in such scenarios, Alpha-Beta Pruning stands out as a pivotal strategy. This technique optimizes the Minimax algorithm, which is fundamental in games like chess and checkers. Let's delve into the nuances of Alpha-Beta Pruning and explore how it streamlines decision-making processes in AI.

Understanding the Minimax Algorithm

Before we can appreciate Alpha-Beta Pruning, we must first understand the Minimax algorithm. This algorithm is used in two-player games to determine the optimal move for a player assuming that the opponent is also playing optimally.

Minimax Basics:

The Minimax algorithm explores all possible moves in a game tree—a diagram representing all potential moves and their outcomes. The algorithm alternates between minimizing and maximizing levels, depending on which player's turn it is. The maximizing player aims to maximize their score, while the minimizing player aims to minimize the score of the maximizing player.

Game Tree Structure:

At each node of the game tree, the Minimax algorithm evaluates the game’s potential outcomes. Each move leads to a new node, expanding the tree further. This exhaustive search helps the algorithm determine the best move at the current game state.

• The Challenge of Game Trees

While Minimax provides a robust method for optimal decision-making, it becomes computationally expensive as the game tree grows. For complex games like chess, the number of possible moves can become astronomical, making it impractical to evaluate every single branch. This is where Alpha-Beta Pruning comes into play.

Introducing Alpha-Beta Pruning

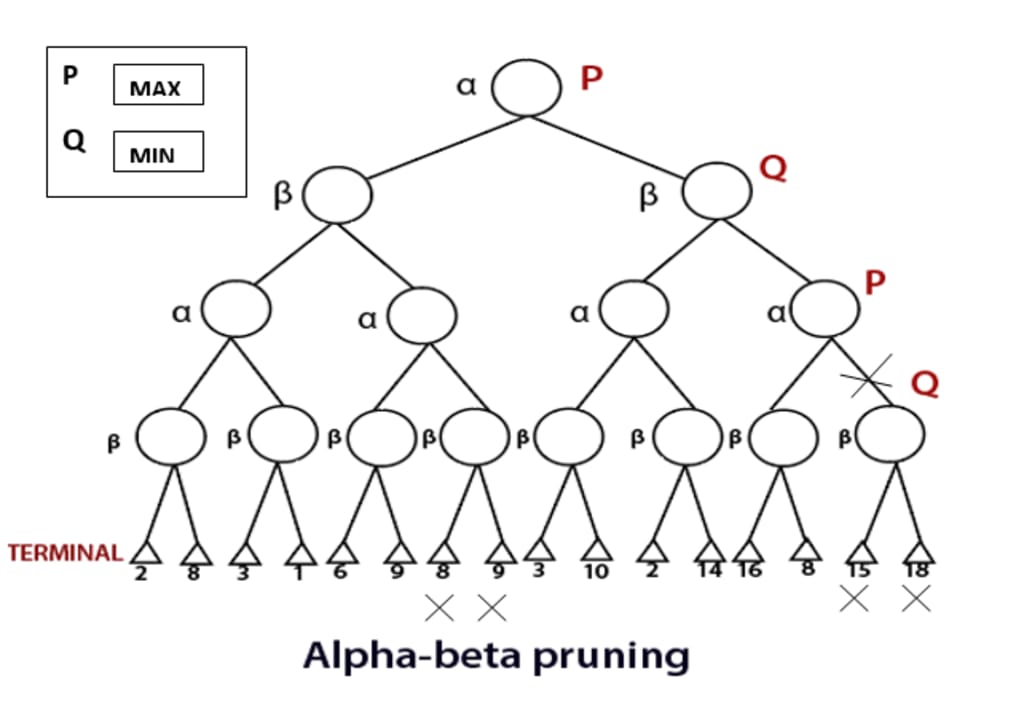
Alpha-Beta Pruning is an enhancement to the Minimax algorithm that significantly reduces the number of nodes evaluated in the search tree. It achieves this by "pruning" or eliminating branches that cannot influence the final decision, thus streamlining the process.

Alpha and Beta Values: Alpha-Beta Pruning introduces two values—alpha and beta—to the Minimax algorithm:

Alpha represents the minimum score that the maximizing player is assured of. It is initially set to negative infinity.

Beta represents the maximum score that the minimizing player is assured of. It is initially set to positive infinity.

During the search, these values are updated as follows:

Alpha is updated to reflect the best score found so far for the maximizing player.

Beta is updated to reflect the best score found so far for the minimizing player.

Pruning Logic: As the algorithm explores the game tree, it uses these alpha and beta values to decide whether to continue exploring a particular branch:

If a branch’s score is worse than the alpha value (for the maximizing player) or better than the beta value (for the minimizing player), further exploration of that branch is unnecessary. This is because the outcome of that branch will not influence the final decision.

How Alpha-Beta Pruning Works

To understand Alpha-Beta Pruning better, let’s break down the process:

Initialization: Start with alpha as negative infinity and beta as positive infinity.

Recursive Search: Traverse the game tree using a depth-first search approach. At each node:

Update alpha or beta values based on the current node’s score.

If alpha is greater than or equal to beta at any node, prune the remaining branches.

Backpropagation: After evaluating a node, propagate the alpha and beta values up the tree. This helps in deciding which branches can be pruned in higher levels of the tree.

Benefits and Applications

Alpha-Beta Pruning offers several advantages:

Efficiency: It reduces the number of nodes that need to be evaluated, thus speeding up the search process.

Scalability: By pruning unnecessary branches, it enables AI to handle more complex game scenarios with a larger branching factor.

This technique is extensively used in classic board games such as chess and checkers, where the complexity of the game tree necessitates efficient searching algorithms. Beyond games, Alpha-Beta Pruning principles are applicable in various decision-making problems where game-like structures are present.

Conclusion

Alpha-Beta Pruning represents a significant advancement in the realm of AI and game theory. Optimizing the Minimax algorithm enhances decision-making efficiency in complex situations. As AI progresses, methods such as Alpha-Beta Pruning are essential for creating systems that address complicated issues effectively.

For both game enthusiasts and AI researchers, grasping the concept of Alpha-Beta Pruning offers significant understanding of intelligent decision-making processes and the continuous advancement of artificial intelligence.