The Power of Exponential Growth: Why Folding a Paper 43 Times Reaches the Moon and Beyond

Directions:

Take a piece of paper and fold it in half. How many layers is it? (2)

Fold it in half again. How many layers is it now? (4)

Fold it in half again. How many layers now? (8)

What do you expect to happen if you fold it in half a fourth time? (16 layers)

Can you identify the pattern? (if n is the number of times you folded, the pattern is 2^n, or 2 x 2 x 2 x 2 x… n times)

A piece of paper is about 0.1 mm thick. Using the pattern you came up with previously, can you figure out how thick the stack is after 2 folds? After 3 folds? After 10 folds? (use 0.1 x 2^n) (answers: 0.2 mm, 0.4 mm, and 102.4 mm)

What is the thickness after 42 folds? The distance between the earth and the moon is around 384,400 kilometers (remember 1 km = 1,000,000 mm). After 42 folds, would the paper reach the moon? (439,804,651,110.4 mm = 439,804.7 km, so yes, it would reach the moon because 439,804.7 > 384,400)

Think Like A Scientist:

How many times can you actually, physically fold the paper?

Is it possible to fold it 42 times? What stops you from being able to fold it this many times?

Is there any way to fix this problem so that you could fold the paper more times?

How It Works:

In this experiment, you learned about exponential growth! This type of growth is called exponential because the equation to model this is 2^n, which is some number (in this case the number 2) raised to an exponent (n). Exponential growth can start small, but then will get big very very quickly! In this example, with each fold, you double the layers of paper you had in the previous fold. In other words, you multiply the layers by 2 each time you fold. This graph gives a visual representation of how fast the thickness of the paper grows.

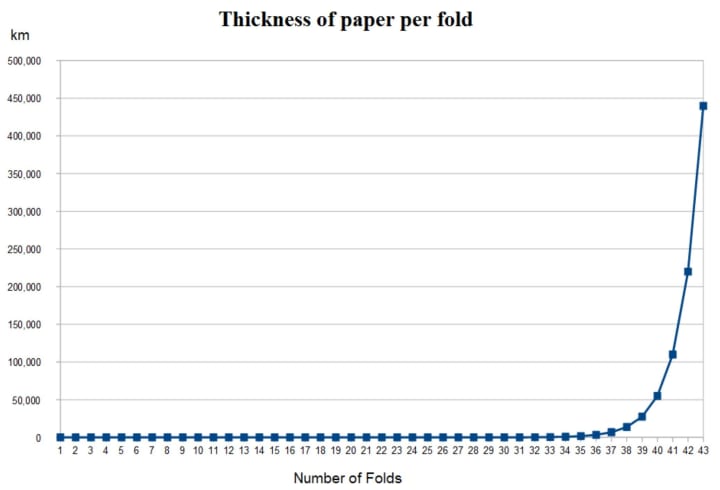
First, notice that along the vertical axis, every line represents 50,000 km. Given that our paper starts at 0.1 mm = 0.0000001 km, you can’t really see the increase in thickness for folds 1-35 on this graph. However, once you get to 36 folds we can notice the increase, and then it grows very fast! We can see this because the line suddenly curves up very steeply, and by 43 folds it is almost at 450,000 km!

Reference

Number of Times You Can Fold a Piece of Paper in Half

The commonly accepted wisdom is that you can't fold a single sheet of paper in half more than seven times.

The problem with folding paper in half multiple times is that the paper's surface area decreases by half with each fold. A single sheet of paper may be easy to cut, rip, or tear, but a paper that has been folded in half multiple times becomes very strong because of the increase in density.

The sevenfold limit holds true if you are using a standard size sheet of printer paper. However, if you alter the size or thickness of the paper, you can increase the number of folds that are possible.​

MythBusters, a popular science program on the Discovery Channel, once featured the paper folding myth on its program. They determined that using a larger sheet of paper would make it possible to fold the paper in half more than seven times. MythBusters used a sheet of paper the size of a football field. By fold seven, everyone involved in the project finds it very difficult. However, the team eventually manages to fold the paper eight times with no tools. With the assistance of a forklift and steamroller, they get the paper to fold 11 times.

In 2001, high school student Britney Gallivan of Pomona, California, successfully managed to fold a paper in half 12 times by using a roll of long, thin specialty toilet paper that was 1.2 kilometers in length. Her efforts were part of an extra credit project for a math class, in which she was challenged to fold anything in half 12 times. She first succeeded using thin gold foil and alternate directions of folding. Later, her teacher asked her to try the folding experiment with paper.

In 2012, a group of math students from St. Mark's School in Southborough, Massachusetts, attempted to set a new paper folding world record by folding a toilet paper in half 13 times with help from their teacher James Tanton. However, unlike Britney Gallivan, they had taped together multiple rolls to make the toilet paper the required 1.2 kilometers. Since paper that is taped together isn't as strong as a single sheet, there is some debate as to whether this should count as a record-breaking attempt.

reference