What is the Fibonacci series?

The Fibonacci series is a set of positive integers in which the first two terms are 0 and 1, respectively, and the third is found by adding the previous two terms.

So, the third term becomes 1 again, as 0 + 1 equals one. However, after the third term, the series starts ascending.

It is because the sum of the second and third terms becomes 2. Similarly, the sum of the third and fourth becomes 3.

Moreover, following the same trend, the series keeps increasing in ascending order. For example, the first eight terms of the Fibonacci series are 0, 1, 1, 2, 3, 5, 8, 13.

Let’s dive into the concept of the Fibonacci Series!

The Historical Significance of the Fibonacci Series

The Fibonacci series was discovered by the famous Italian mathematician Leonardo Fibonacci. Leonardo Fibonacci was famous as the man who told Europe about the Hindu Arabic numeral system.

It is believed that he invented the Fibonacci series to track the growth of the rabbits' population. However, the other significant uses of the Fibonacci series and its discovery in nature were not done by Fibonacci.

After some time, when this series caught the eyes of scholars and mathematicians, its uses and significance were discovered.

The Fibonacci series soon helped to discover new areas of multiple branches of mathematics. Moreover, it also revolutionized the subject of computer science.

Applications of Fibonacci Series in Real World

The Fibonacci series has multiple real-world uses in many fields. So let's discuss its applications in different fields, including the field of programming.

Financial Analysis

Traders and investors use the Fibonacci series to study market trends and make decisions about buying and selling stocks. It helps them find important levels where prices might go up or down.

Nature and Biology

The Fibonacci series can be found in nature like the way leaves grow on stems or how shells and galaxies are shaped. It shows how nature follows a pattern that is both beautiful and efficient.

Computer Graphics and Design

Designers use the Fibonacci series to create visually pleasing designs in computer graphics, art, and architecture. It helps them create balanced and harmonious layouts.

Mathematics and Number Theory

Mathematicians study the Fibonacci series to understand numbers better. It helps them explore different mathematical concepts and patterns. It is also used as an educational tool to teach math.

These examples show how the Fibonacci series is used in many practical ways outside of math. It connects different fields like finance, nature, design, programming, math, and art. It helps to understand and appreciate the world in a deeper way.

Applications of the Fibonacci Series in Programming

Algorithm Design

The Fibonacci series helps to learn important programming techniques. It includes recursion, iteration, and dynamic programming.

Performance Testing

Performance testing is one of the most important applications of the Fibonacci series. Generating Fibonacci numbers is often used to test programming languages, compilers, and hardware.

Sequence Generation

The Fibonacci series is a starting point for creating other important sequences. By using the Fibonacci sequence, you can generate sequences like the Lucas series and the Pell series. These sequences have been used in cryptography, graph theory, and coding theory.

Algorithmic Optimization

The Fibonacci series helps to create improved algorithms for generating Fibonacci numbers.

Fibonacci Series in Python

As you already learned, the Fibonacci series helps programming beginners to learn about recursion, iteration and dynamic programming, so let's briefly discuss the generation python Fibonacci series.

Generation of the Fibonacci series in Python through iteration

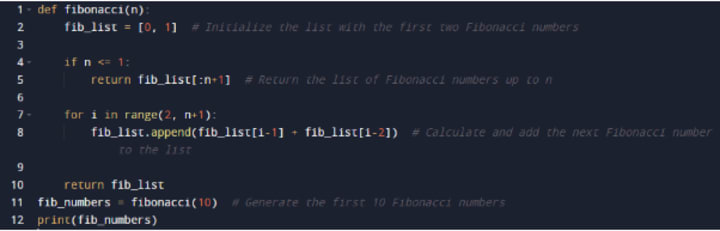
Input

In this program, a function called `fibonacci` takes an integer `n` as input, representing the terms of the Fibonacci series in Python to generate.

It starts by initializing a list `fib_list` with the first two Fibonacci numbers, which are 0 and 1. Next, it checks if `n` is less than or equal to 1. If so, it returns a portion of the `fib_list` containing the required number of Fibonacci numbers. This handles the special cases where `n` is 0 or 1.

If `n` is greater than 1, it enters a `for` loop that iterates from 2 to `n`. Inside the loop, it calculates the next Fibonacci number by adding the last two numbers in the `fib_list`, which are `fib_list[i-1]` and `fib_list[i-2]`. It then appends this new number to the `fib_list`.

After the loop completes, it returns the complete `fib_list`, which contains all the generated Fibonacci numbers. To use this program, you can call the `Fibonacci` function with the desired value of `n` and store the returned list of Fibonacci numbers in a variable as given in the 10th to 12th line of code.

This program generates the Fibonacci series in Python iteratively by starting with the first two numbers and progressively calculating and adding the next numbers in the series until the desired number of Fibonacci numbers is reached.

Output

What is an online Python compiler?

An online Python compiler is a special tool you can use on the internet to write and run Python code without needing to install anything on your computer.

It works right in your web browser, which means you can access it from anywhere with an internet connection. With an online Python compiler, you can type your Python code, run it, and see the results immediately.

It's like having a virtual Python environment online. These compilers are handy because they save you the trouble of setting up a programming environment on your computer.

They also let you share your code with others by simply sending them a link. Moreover, Online Python code compilers are designed to be user-friendly.

Summing Up

The Fibonacci series is one of the most fascinating concepts of mathematics. However, this fascination is not limited to mathematics only.

The application of the Fibonacci series can also be seen in the fields like biology, art and even programming.

In programming, it can be your great partner who will help you with countless algorithms in programming.