Minimization With Constraints Using Python’s SymPy

Today, I will apply SymPy to a simple minimization problem with constraints. In particular, I will use the method of Lagrange multipliers. If you are familiar with this method, you can skip the following section and jump to the second section where I will solve the problem using SymPy.

The problem to solve is as follows: What is the shortest distance between the origin and the curve

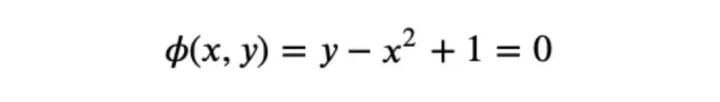
Minimization with constraints: Lagrange multipliers

The squared distance from the point (𝑥,𝑦) to the origin is:

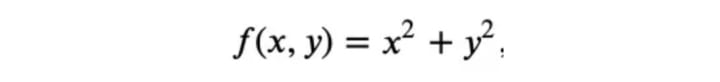
So, we have to minimize 𝑓 in some way. But not all 𝑥 and 𝑦 are allowed. Only those 𝑥,𝑦 that satisfy 𝜙(𝑥,𝑦)=0 are valid. The most general way of solving this kind of problem is by the method of Lagrange multipliers, which I will shortly summarize.

So, we have to minimize 𝑓 in some way. But not all 𝑥 and 𝑦 are allowed. Only those 𝑥,𝑦 that satisfy 𝜙(𝑥,𝑦)=0 are valid. The most general way of solving this kind of problem is by the method of Lagrange multipliers, which I will shortly summarize.

So we want to minimize 𝑓. For a minimum (or maximum), the differential vanishes:

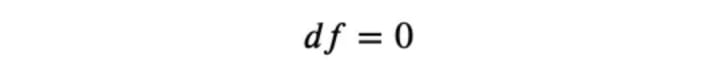
Also, since 𝜙 is a constant function, we have

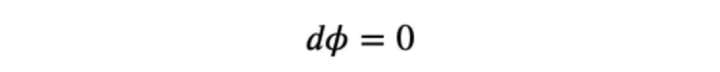
Hence, it is true that for any 𝜆

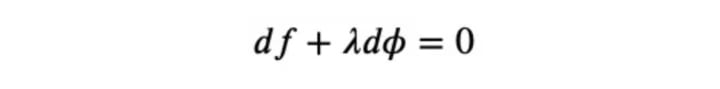
or explicitly:

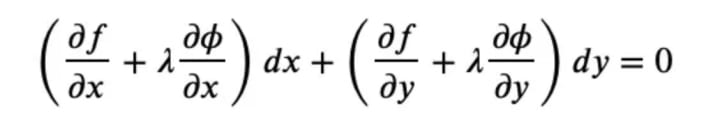
Since this is true for any 𝜆, we can say that we choose one that makes the second braces equal to zero. Hence, also the first braces must be equal to zero. So we have to solve

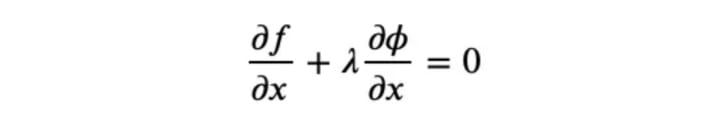
and

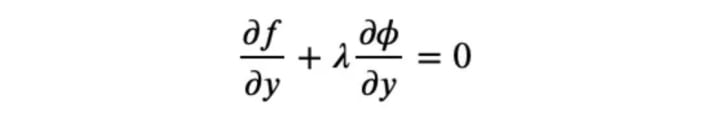
and

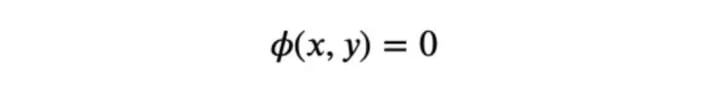
for 𝑥,𝑦, and 𝜆. Well, we don’t have to solve for 𝜆 because we are not interested in it, but often it makes the algebra simpler to calculate 𝜆 and plug it into the equations.

Anyways, now comes the SymPy part.

Solving the problem with SymPy

As usual, we start by opening a Jupyter notebook and conveniently import SymPy:

Importing everything from sympy.abc saves us from defining one-letter symbols like 𝑥 explicitly.

Define our constraint:

In Jupyter notebooks, you can use Greek symbols as variable names. To do this, enter the LaTeX name of the letter, e.g. \phi and press TAB. This will convert the letter into the corresponding Unicode symbol.

Then define the distance function to minimize:

Next, we need to calculate the differentials. It seems that there is no function in SymPy for that, the closest I have found is idiff, but that can only handle the case for two variables. That would suffice for our problem, but would not generalize to more variables, so I prefer to write my code. The first function gives me the symbol for the differential, 𝑑𝑥, of some variable 𝑥:

So when I enter d(y) it gives me 𝑑𝑦.

We have to compute differentials of functions like 𝑑𝑓 in terms of differentials of variables like 𝑑𝑥 and 𝑑𝑦. This can be achieved by the following little function:

So for 𝑑𝑓+𝜆𝑑𝜙, we have

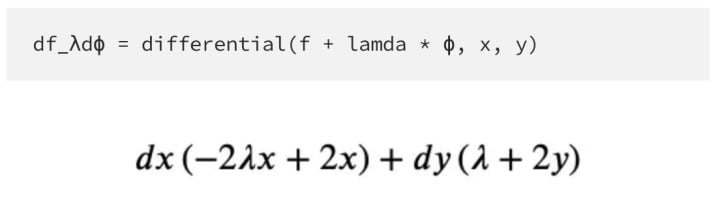
We need the terms behind the differentials. How can we access these subexpressions? The simplest way is by accessing the args property of the expression:

which gives:

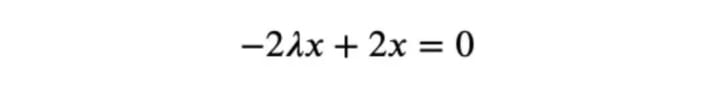
and

which gives:

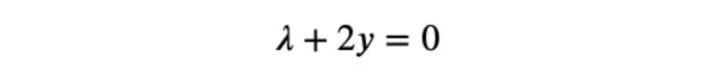
However, it is quite cumbersome to use the args property, because you always have to try out which index to take. It is more convenient and powerful to use pattern matching instead. To do this, define two SymPy-wildcards:

Then use the wildcards to match the braces in the expression df_λdϕ:

which yields:

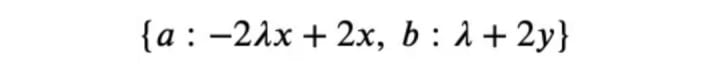
As you can see, the braces after the 𝑑𝑥 have been matched to 𝑎 and the second one to 𝑏 as intended. So we can write:

which gives the same results as the raw approach with args.

The third equation is simply the constancy of 𝜙:

Now we can solve these three equations for the three unknowns:

These are the candidates for the point of minimum distance from the origin. But which ones are minima and not maxima? To distinguish the points, we choose a simple approach: just calculate the distance from origin at those candidate points.

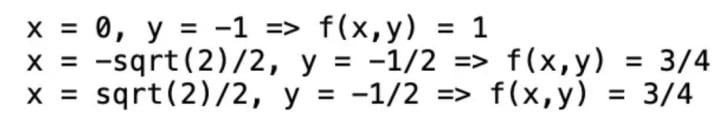
The distance at the two points

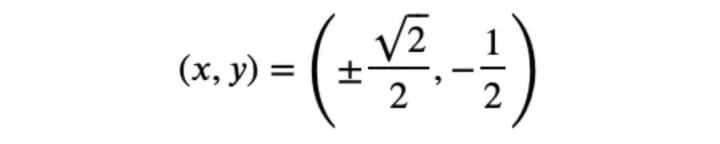
is lower than at (𝑥,𝑦)=(0,−1). And since 𝑓 and 𝜙 are continuous, the former two points must be the minima.

That’s it about this problem. I think the most important takeaway of SymPy techniques is the wildcard approach because matching subexpressions will occur in any kind of problem. As usual, if you have an idea how to do this problem more elegantly with SymPy, please post a comment.