What is a Threaded Binary Tree?

In the world of computer science and data structures, trees play a critical role in organizing information for efficient access and manipulation. Among various types of binary trees, the Threaded Binary Tree stands out due to its unique structure designed to make tree traversal more efficient without requiring additional memory overhead. This article delves into what a threaded binary tree is, why it’s useful, and how it differs from conventional binary trees.

Understanding the Binary Tree Basics

Before diving into the concept of a threaded binary tree, it is important to understand the basics of a binary tree. A binary tree is a hierarchical data structure where each node has at most two children—often referred to as the left and right children. Common operations on a binary tree include insertion, deletion, and traversal. The most frequent traversals are inorder, preorder, and postorder.

Inorder Traversal in Binary Trees

In inorder traversal, the process is:

Traverse the left subtree.

Visit the root node.

Traverse the right subtree.

In a typical binary tree, this traversal is often implemented using recursion or a stack to backtrack after visiting the left subtree. However, both approaches require extra space, which becomes inefficient for large trees.

This is where threaded binary trees come into play.

What is a Threaded Binary Tree?

A Threaded Binary Tree (TBT) is a variation of the binary tree that eliminates the need for stack-based backtracking during tree traversal. In a standard binary tree, many of the child pointers are NULL, especially in leaf nodes (which have no children). A threaded binary tree takes advantage of these null pointers by replacing them with pointers to inorder predecessors or inorder successors. These additional links are called “threads.”

The main idea behind this structure is to make inorder traversal faster by avoiding recursive calls or the use of external data structures.

Types of Threaded Binary Trees

There are two main types of threaded binary trees:

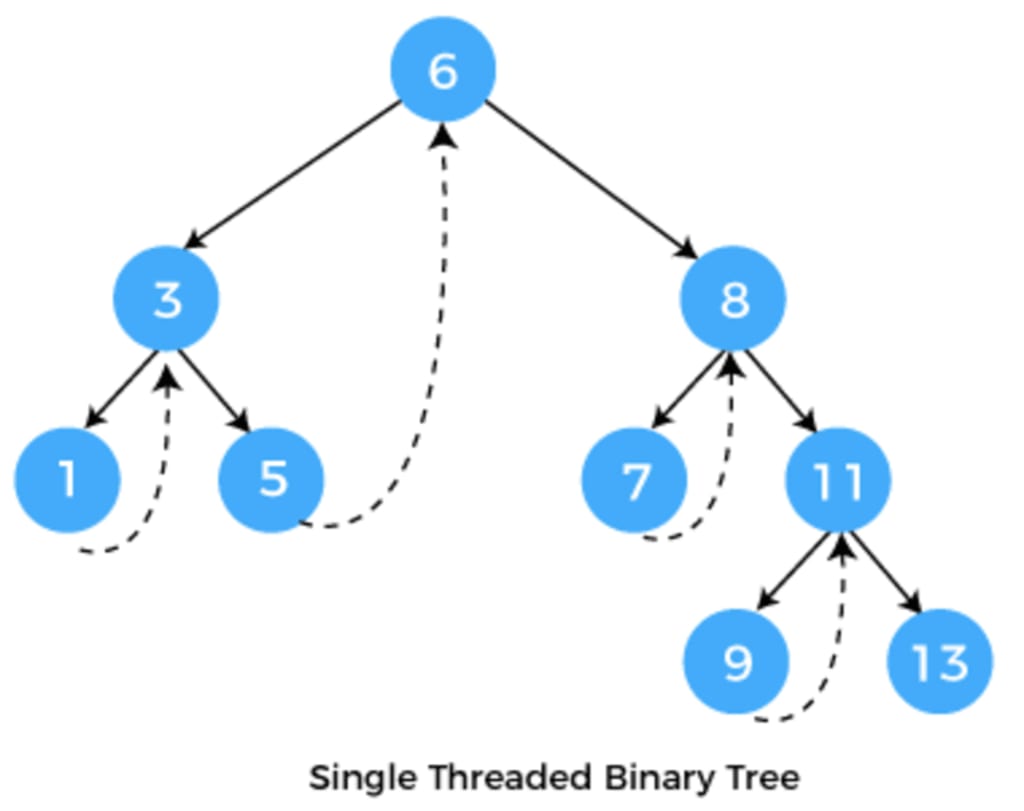
Single-Threaded Binary Tree:

In this type, either the NULL left or right pointer is replaced by a thread.

If the left pointer is NULL, it can point to the inorder predecessor of the node.

If the right pointer is NULL, it points to the inorder successor of the node.

Double-Threaded Binary Tree:

In a double-threaded tree, both left and right NULL pointers are replaced by threads.

This means each node contains a thread for both its inorder predecessor (using the left pointer) and its inorder successor (using the right pointer).

Example

Consider the following binary tree for illustration:

markdown

Copy code

10

/ \

5 15

/ \ / \

3 7 12 20

In a threaded binary tree, the NULL left pointer of node 3 could point to the node's inorder predecessor (in this case, 5), and the NULL right pointer of node 7 could point to its inorder successor (in this case, 10). This threading mechanism allows the inorder traversal to directly move from one node to its next without recursion or an explicit stack.

Benefits of Threaded Binary Trees

Efficient Traversal: The most significant advantage of a threaded binary tree is the speed and efficiency of traversal. Inorder traversal becomes simpler and faster as there’s no need to maintain a stack or use recursion. The threads allow direct movement from one node to its successor or predecessor.

Reduced Memory Overhead: Because the tree takes advantage of the already existing NULL pointers, there’s no need for additional structures like stacks during traversal. This reduces the memory overhead, especially for large trees.

Simplified Algorithms: Threaded trees simplify the implementation of certain algorithms, especially those involving traversal. With proper threading, iterative traversal can be achieved without complex coding.

Minimal Extra Space: Since threading only involves utilizing existing NULL pointers, it doesn’t require significant additional space.

Limitations

Insertion and Deletion Complexity: While traversal is optimized, insertion and deletion operations can become more complicated due to the presence of threads. Care must be taken to correctly update these threads when a node is added or removed.

Extra Complexity in Construction: Initially building a threaded binary tree involves more work than building a standard binary tree, since threads need to be correctly assigned during tree construction.

Use-Case Dependent: Threaded binary trees are particularly beneficial when traversal is a frequent operation, but they may not offer significant advantages in cases where the focus is more on insertion and deletion.

Practical Applications

Threaded binary trees are useful in applications where space is limited or where fast, non-recursive traversal is needed. They can be found in scenarios like:

Database indexing: Where efficient access and minimal memory usage are critical.

Compiler design: For syntax trees where frequent inorder traversal is needed.

Symbol tables: In interpreters and other data structures used in compilers.

Conclusion

A threaded binary tree offers a clever way to optimize tree traversal by utilizing the otherwise wasted NULL pointers in standard binary trees. By pointing these NULLs to inorder predecessors and successors, threaded trees can achieve fast and memory-efficient inorder traversal. Although more complex to implement, they offer significant performance advantages, especially in systems where traversal is a frequent operation.