Set Shaping Theory

In this article, we will introduce set shaping theory a new and promising method of data compression. The purpose of this method is the encoding of the message in the absence of information on the source that generated it. This method uses a new class of function that transform the sequence to be encoded into a new sequence of greater length. This Operation is called “shaping of the source” and the difference in length between the initial message and the transformed one is called the “shaping order of the source”.

In order to understand this compression technique it is important to introduce the zero order empirical entropy.

Given a sequence s, of random variables, of length N, with p(si) the frequency of the symbol si in the sequence, we call zero order empirical entropy H0(s) the following function:

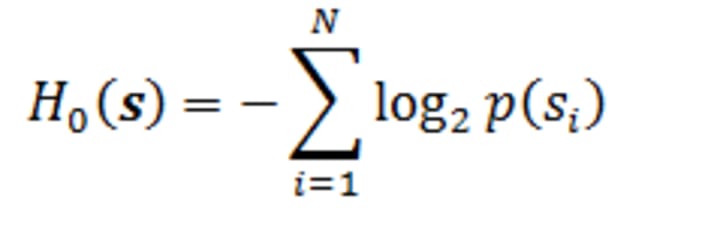
This function tell us that a sequence s of random variables of length N on average cannot be encoded in less than NH0(s) bits and therefore, it represents the sequence information content.

If we call S the set that contains all the sequences of length n belonging to an alphabet A. The set shaping theory tells us that there exists a set Y of equal size to S with sequences of greater length N2 which have an average value of N2H0(y) and less than NH0(s). Having the two sets the same size; it is possible to generate a one-to-one correspondence between the sequences belonging to the two sets.

Therefore, by applying this transformation we can with a probability greater than fifty percent to transform a sequence s in a new sequence y which can be encoded with a number of bits less than to NH0(s).

If the zero order empirical entropy multiplied by the length of the message defines the encoding limit, how is it possible to overcome it? It defines a limit under particular conditions, in other words, it defines the encoding of the source, in fact, it is called source coding theorem. The encoding of the message is something slightly different. A common mistake is to consider message encoding and source encoding the same thing. Shannon's theorem is about coding the source, which means developing the coding code (codewords) before the message is generated. On the other hand, in the set shaping theory the source does not exist, there is only the message that must be transmitted, therefore it faces the problem from a more general point of view. In fact, the knowledge of the source that generated the message is an optional information; in many cases it is not known.

To better understand this result we recommend reading this article which explains the implication of this result on Shannon's first theorem.

A breakthrough in the study of this new theory was made when a group of information theory students first succeeded in applying this theory. In this way, they were able to experimental validate the theoretical predictions.

They shared the code, which can be downloaded and used by anyone.

The data compression experiment is brilliant because it makes us understand the difference between source encoding and message encoding.

The program performs the following steps:

1) randomly generate a sequence s with uniform distribution

2) calculate the actual frequencies of the symbols present in s

3) use this information to calculate the zero order empirical entropy

4) apply the set shaping theory

5) apply the Huffman coding

6) compares the zero order empirical entropy of s with the length of the encoded transformation sequence

7) repeats all these steps a statistically significant number of times

8) displays all the average results obtained

The gains obtained by applying this technique are always less than the number of bits necessary to describe the coding scheme (codewords list). Therefore, the result obtained does not allow to compress a random sequence in fact, any information that is not independent from the message must be transferred to the decoder. According to this new theory the compressed message is defined by its encoding plus the coding scheme this new approach adapts better to what happens from the experimental point of view in which both this information is sent to the decoder.