"Mastering Regularization Techniques: Enhancing Model Performance and Generalization"

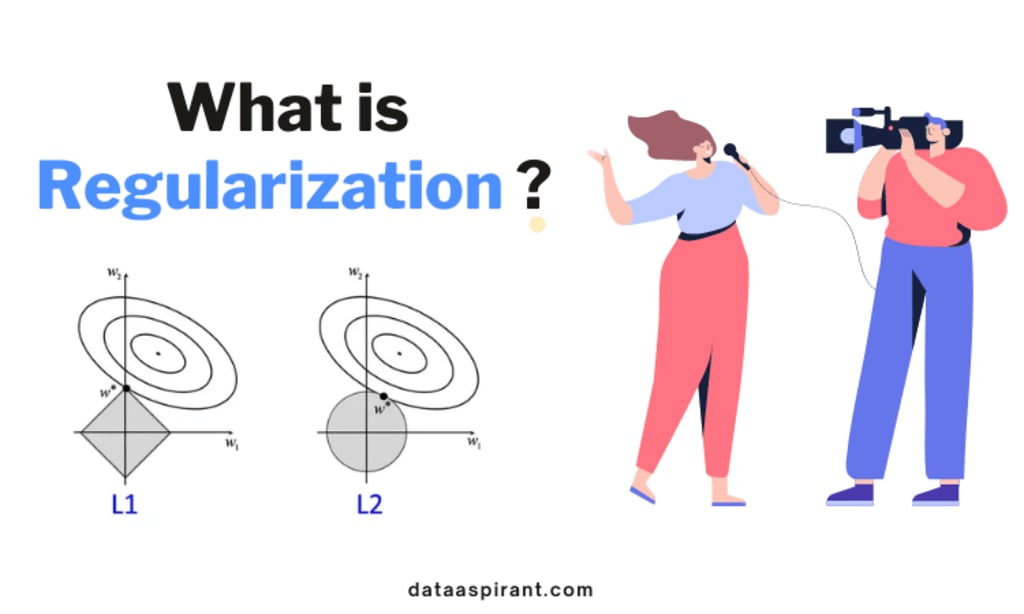
Regularization is a technique used in machine learning to prevent overfitting, which occurs when a model becomes too complex and performs well on the training data but poorly on new, unseen data. It helps to find a balance between capturing the patterns in the training data and generalizing well to new data.

In simple terms, regularization adds a penalty term to the model's objective function, encouraging it to keep the model weights small or sparse. This penalty discourages the model from relying too heavily on any particular feature or from fitting the noise in the training data.

Let's consider an example to understand regularization in the real world. Suppose you want to predict housing prices based on various features such as size, number of bedrooms, location, etc. You have a dataset with a limited number of housing examples.

Without regularization, a model might become overly complex and try to fit the noise or outliers in the training data. This can lead to poor performance when predicting housing prices for new, unseen data.

By applying regularization, you can control the complexity of the model. One common type of regularization is called L2 regularization or ridge regression. It adds a penalty term to the model's objective function, which is proportional to the square of the weights of the model. This encourages the model to keep the weights small.

So, in the case of predicting housing prices, regularization would help prevent the model from assigning excessive importance to any particular feature. It would ensure that the model doesn't overly rely on, for example, the number of bathrooms in a house, but instead considers a balanced combination of all relevant features.

Overall, regularization helps to generalize the model's predictions by avoiding overfitting and promoting a more balanced representation of the data.

Ridge regression

Ridge regression is a technique used for linear regression with regularization. It addresses the issue of multicollinearity, where the independent variables are highly correlated with each other. The goal of ridge regression is to find the best-fit line that minimizes the sum of squared errors while also considering the magnitude of the coefficients.

In simple linear regression with two variables y and x, the relationship between them is represented by the equation:

y = mx + b

where m is the slope and b is the y-intercept. In ridge regression, we introduce a regularization term to the ordinary least squares (OLS) objective function, which helps to control the magnitude of the coefficients.

The regularized objective function for ridge regression is:

J(m, b) = Σ(yi - mx - b)² + λm²

where Σ denotes the sum over all data points, λ is the regularization parameter, and m² is the squared magnitude of the slope term.

To derive the ridge regression equation, we start by differentiating the objective function with respect to b:

∂J(m, b) / ∂b = -2Σ(yi - mx - b)

Setting this derivative equal to zero and solving for b, we get:

0 = -2Σ(yi - mx - b) 0 = Σyi - mΣxi - nb

Dividing by n (the number of data points) and rearranging the equation, we find:

b = y_bar - mx_bar

where y_bar is the mean of the dependent variable y and x_bar is the mean of the independent variable x.

Next, we substitute the derived value of b into the objective function:

J(m) = Σ(yi - mx - (y_bar - mx_bar))² + λm²

Expanding the squared term, we have:

J(m) = Σ(yi - mx - y_bar + mx_bar)² + λm² J(m) = Σ(yi - y_bar - mx + mx_bar)² + λm² J(m) = Σ((yi - y_bar)² - 2(yi - y_bar)(mx - mx_bar) + (mx - mx_bar)²) + λm²

Simplifying, we can rewrite the equation as:

J(m) = Σ(yi - y_bar)² - 2mΣ(xi - x_bar)(yi - y_bar) + m²Σ(xi - x_bar)² + λm²

To find the optimal value of m, we differentiate J(m) with respect to m:

∂J(m) / ∂m = -2Σ(xi - x_bar)(yi - y_bar) + 2mΣ(xi - x_bar)² + 2λm

Setting this derivative equal to zero and solving for m, we get:

0 = -2Σ(xi - x_bar)(yi - y_bar) + 2mΣ(xi - x_bar)² + 2λm 2mΣ(xi - x_bar)² + 2λm = 2Σ(xi - x_bar)(yi - y_bar) m(Σ(xi - x_bar)² + λ) = Σ(xi - x_bar)(yi - y_bar)

Finally, solving for m, we have:

m = (Σ(xi - x_bar)(yi - y_bar)) / (Σ(xi - x_bar)² + λ)

This is the final equation for the slope term in ridge regression. It takes into account the regularization parameter λ, which helps control the magnitude of the coefficient.

If we increase the value of the regularization parameter λ in ridge regression, it has two main effects:

1. Impact on the slope (m): As λ increases, the impact on the slope term becomes more significant. The numerator of the equation, Σ(xi - x_bar)(yi - y_bar), remains the same, but the denominator, Σ(xi - x_bar)² + λ, increases. As a result, the magnitude of the slope (m) decreases. Increasing λ penalizes larger values of m, leading to a shrinkage effect on the coefficient estimates. This helps in reducing the overfitting tendency by preventing the coefficients from taking excessively large values.
2. Impact on overfitting: Overfitting occurs when the model becomes too complex and fits the training data too closely, leading to poor generalization to new, unseen data. Increasing λ in ridge regression can help reduce overfitting. By penalizing the magnitude of the coefficients, ridge regression shrinks them towards zero. This shrinking effect reduces the complexity of the model, making it less sensitive to variations in the training data. Consequently, ridge regression can help improve the model's ability to generalize well to new data, thus reducing overfitting.

In summary, increasing the regularization parameter λ in ridge regression decreases the magnitude of the slope term (m) and helps alleviate overfitting by shrinking the coefficients towards zero.

have started implementing the MeraRidge class for ridge regression

class MeraRidge:

def __init__(self, alpha=0.1):

self.alpha = alpha

self.m = None

self.b = None

def fit(self, X_train, y_train):

num = 0

den = 0

for i in range(X_train.shape[0]):

num += (y_train[i] - y_train.mean()) * (X_train[i] - X_train.mean())

den += (X_train[i] - X_train.mean()) ** 2

self.m = num / (den + self.alpha)

self.b = y_train.mean() - (self.m * X_train.mean())

print("Coefficients (m, b):", self.m, self.b)

def predict(self, X_test):

if self.m is None or self.b is None:

raise Exception("Model has not been trained. Please call fit() first.")

y_pred = self.m * X_test + self.b

return y_pred

100-days-of-machine-learning/ridge-regression-key-understandings.ipynb at main · campusx-official/100-days-of-machine-learning · GitHub

"The Impact of Increasing Lambda on Coefficients: Exploring Regularization from 0 to Infinity"

When the value of lambda (regularization parameter) is increased from 0 to infinity in ridge regression, it has a significant impact on the estimated coefficients (m) of the model. Here's how the coefficients are affected:

As lambda increases:

• The impact of the regularization term becomes stronger.
• The coefficients are penalized more heavily for being large.
• The magnitude of the coefficients tends to decrease towards zero.

When lambda is close to infinity:

• The impact of the regularization term dominates the objective function.
• The coefficients are pushed towards zero as much as possible.
• This results in a flatter model with significantly smaller coefficients.

In essence, increasing lambda in ridge regression introduces more regularization, which helps to reduce the influence of high-variance features and mitigate overfitting. The higher the value of lambda, the stronger the regularization effect, and the more the coefficients shrink towards zero.

It's important to note that very large values of lambda can lead to excessively small coefficients, potentially resulting in underfitting. Therefore, the choice of an appropriate lambda value should be based on cross-validation or other model evaluation techniques to find the right balance between bias and variance in the model.

higher values of coffiecties like x1 has w1=100,x2 hs w2 50,x3 has w3 10,x1 is fastky decrese are impacted more they decrease fast toward zero explain it in easy way and fast

In ridge regression, when we have higher values of coefficients (weights) for certain features, such as w1 = 100 for x1, w2 = 50 for x2, and w3 = 10 for x3, those coefficients are impacted more and tend to decrease faster towards zero when we increase the value of lambda.

Imagine we have a dataset with features x1, x2, and x3. The coefficients w1, w2, and w3 represent the weights assigned to each feature. A higher weight means that the corresponding feature has a stronger influence on the predicted outcome.

When we increase lambda in ridge regression, we are increasing the strength of regularization, which penalizes large coefficients. In this case, the high weights of w1 = 100 and w2 = 50 make x1 and x2 more influential in determining the outcome compared to x3 with w3 = 10.

As lambda increases, the impact of the regularization term becomes stronger. It forces the model to shrink the coefficients towards zero. However, the magnitude of the coefficients is affected differently due to their initial values.

Since w1 = 100 is much larger compared to w2 = 50 and w3 = 10, it will be penalized more heavily by the regularization term. Therefore, the coefficient w1 will decrease faster compared to w2 and w3. This rapid decrease aims to reduce the influence of x1 in the model and prevent it from dominating the predictions excessively.

Similarly, w2 = 50 will decrease but at a slower rate compared to w1, and w3 = 10 will decrease at an even slower rate. The coefficients w2 and w3 will decrease, but their initial lower magnitudes make them less affected by the regularization term.

In summary, the higher coefficients (weights) are impacted more by regularization because they have a larger initial influence on the predictions. Increasing lambda amplifies the penalty for large coefficients, causing them to decrease faster towards zero. This process helps to balance the contributions of different features and mitigate the risk of overfitting.

Lasso regression

Lasso regression, short for "Least Absolute Shrinkage and Selection Operator," is a linear regression technique that performs both regularization and feature selection. It is widely used to handle high-dimensional datasets and to identify the most important features contributing to the target variable. Let's delve into how lasso regression achieves feature selection in detail.

Lasso regression introduces a regularization term to the ordinary least squares (OLS) loss function. The regularization term is the sum of the absolute values of the coefficients multiplied by a regularization parameter, lambda (λ). The lasso regression loss function can be defined as follows:

Loss = OLS Loss + λ * (sum of absolute values of coefficients)

The key feature of lasso regression is that it can drive some of the coefficients to exactly zero. This property makes it particularly useful for feature selection. Here's how lasso regression accomplishes feature selection:

1. Shrinking Coefficients: Like ridge regression, lasso regression shrinks the coefficients towards zero. However, unlike ridge regression, lasso regression has the ability to shrink some coefficients to exactly zero.
2. Sparsity and Feature Selection: When the value of lambda is sufficiently large, lasso regression can set the coefficients of less important features to zero. This leads to sparse models, where only a subset of the features is selected for prediction.
3. Automatic Feature Selection: Lasso regression provides an inherent mechanism for automatic feature selection. By examining the resulting non-zero coefficients, you can identify the features that have the most significant impact on the target variable.
4. Handling Multicollinearity: Lasso regression can handle multicollinearity, which occurs when there is high correlation among predictor variables. In the presence of multicollinearity, lasso tends to select one feature from a group of highly correlated features and set the others to zero.
5. Tuning Lambda: The choice of the lambda parameter is crucial in lasso regression. A small lambda leads to results similar to ordinary linear regression, while a large lambda promotes sparsity and more aggressive feature selection. Cross-validation techniques can be used to determine the optimal value of lambda.

By using lasso regression, you can obtain a subset of the most relevant features while simultaneously fitting a regression model. This feature selection capability helps to simplify the model, improve interpretability, reduce overfitting, and enhance predictive performance, particularly in situations with high-dimensional data and a large number of potential predictors.

Elastic Net

Elastic Net is a linear regression technique that combines both L1 and L2 regularization penalties. It is designed to address the limitations of ridge regression and lasso regression, particularly in the presence of multicollinearity. Let's dive into the details of Elastic Net and how it helps in cases of multicollinearity.

Elastic Net combines the L1 (lasso) and L2 (ridge) regularization terms in the loss function. The Elastic Net loss function can be defined as follows:

Loss = OLS Loss + λ1 * (sum of absolute values of coefficients) + λ2 * (sum of squared coefficients)

The Elastic Net regularization term consists of two components: the L1 penalty that encourages sparsity and the L2 penalty that encourages small but non-zero coefficients.

Here's how Elastic Net helps in cases of multicollinearity:

1. Dealing with Multicollinearity: Multicollinearity occurs when there is high correlation among predictor variables. In such cases, ridge regression alone may lead to biased or unstable coefficient estimates. Lasso regression, on the other hand, may arbitrarily select one feature over another. Elastic Net combines the benefits of both techniques to address multicollinearity more effectively.
2. Selection of Relevant Features: Elastic Net can select relevant features and discard irrelevant or redundant ones. The L1 penalty in Elastic Net encourages sparsity, resulting in some coefficients being set exactly to zero. This helps identify and exclude less important features, reducing model complexity and improving interpretability.
3. Balancing L1 and L2 Penalties: The λ1 and λ2 parameters control the strengths of the L1 and L2 penalties, respectively. By appropriately tuning these parameters, Elastic Net can balance between feature selection (sparsity) and shrinkage of coefficients. This flexibility allows for fine-grained control over the regularization process.
4. Tradeoff between Bias and Variance: Elastic Net allows for a tradeoff between bias and variance. Increasing the value of λ1 promotes sparsity, leading to a smaller subset of features with more bias but potentially lower variance. Increasing the value of λ2 encourages shrinkage of coefficients towards zero, reducing variance but possibly introducing more bias. The choice of λ1 and λ2 depends on the specific dataset and the desired tradeoff.
5. Automatic Feature Selection: Similar to lasso regression, Elastic Net provides an inherent mechanism for automatic feature selection. The model can identify the most relevant features by examining the non-zero coefficients. This helps simplify the model, improve interpretability, and reduce the risk of overfitting.

Elastic Net is particularly beneficial in situations where multicollinearity is present and feature selection is desired. By combining the strengths of both L1 and L2 regularization, Elastic Net offers a more robust and flexible approach to regression modeling, striking a balance between bias and variance while effectively handling correlated predictor variables.

In summary, the higher coefficients (weights) are impacted more by regularization because they have a larger initial influence on the predictions. Increasing lambda amplifies the penalty for large coefficients, causing them to decrease faster towards zero. This process helps to balance the contributions of different features and mitigate the risk of overfitting.