Breaking Down Addition and Subtraction Problems

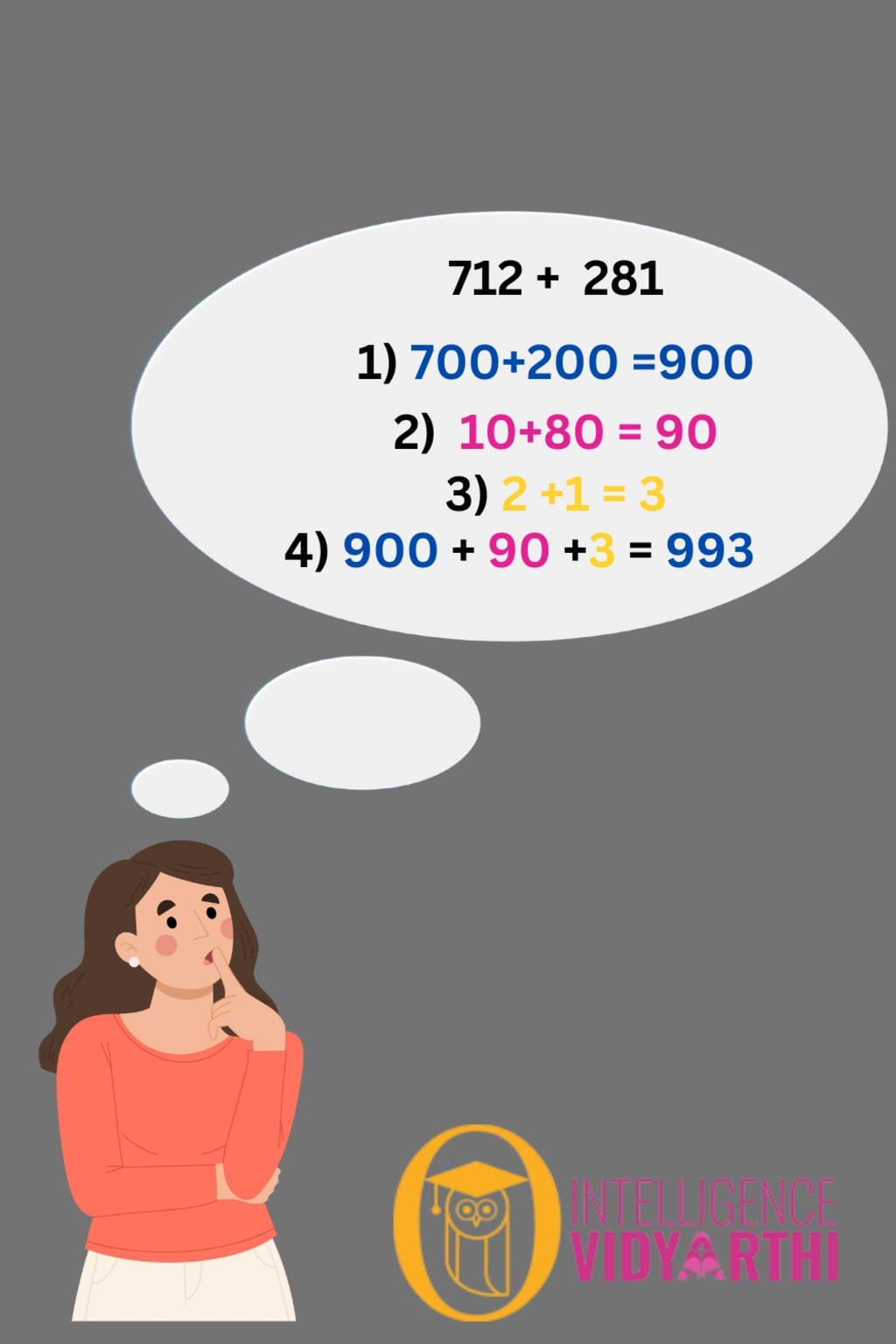
Addition and subtraction are fundamental arithmetic operations, and mastering them is crucial for building a strong mathematical foundation. However, as problems become more complex, it can be challenging to keep track of all the numbers involved. Breaking these problems into smaller, manageable parts can make solving them much easier and more intuitive. In this blog, we’ll explore strategies for dissecting addition and subtraction problems to enhance your problem-solving skills.

1. Understand the Problem

Before you begin solving a problem, take a moment to understand it thoroughly. For example, if you’re asked to calculate 376 + 489, start by visualizing the numbers and the operation. Recognize that you’re combining two quantities to get a total. Similarly, for subtraction like 678–297, you’re finding out how much remains after removing one quantity from another.

mental math

2. Break Down Addition Problems

Addition problems can be simplified by breaking them into parts. Let’s use 376 + 489 as an example:

Break into Hundreds, Tens, and Units:

Separate each number into hundreds, tens, and units:

376 = 300 + 70 + 6

489 = 400 + 80 + 9

Add Each Component Separately:

Add the hundreds: 300 + 400 = 700

Add the tens: 70 + 80 = 150

Add the units: 6 + 9 = 15

Combine the Results:

Add the partial sums together: 700 + 150 + 15 = 865

By breaking the numbers into parts and adding each part separately, you simplify the addition process and reduce the likelihood of mistakes.

3. Break Down Subtraction Problems

Subtraction can also be streamlined using a similar approach. Consider 678–297:

Break into Hundreds, Tens, and Units:

Separate each number:

678 = 600 + 70 + 8

297 = 200 + 90 + 7

Subtract Each Component Separately:

Subtract the hundreds: 600–200 = 400

Subtract the tens: 70–90 (you need to borrow here)

Adjust the tens: 70 + 10 = 80 (from the hundreds)

Now subtract: 80–90 = -10 (so, borrow from the hundreds, making it 400–200 = 300 and so on)

Subtract the units: 8–7 = 1

Combine the Results:

Adjust for any borrowing errors if necessary and combine the parts carefully. For this example: 300 + (-10) + 1 = 291

4. Apply the Strategy to Larger Numbers

This breakdown method can be applied to larger numbers as well. For instance, 2,345 + 1,678:

Break Down:

2,345 = 2,000 + 300 + 40 + 5

1,678 = 1,000 + 600 + 70 + 8

Add Components:

Thousands: 2,000 + 1,000 = 3,000

Hundreds: 300 + 600 = 900

Tens: 40 + 70 = 110

Units: 5 + 8 = 13

Combine Results:

3,000 + 900 + 110 + 13 = 4,023

5. Practice and Patience

Mastering these techniques requires practice. Start with simple problems and gradually move on to more complex ones. The more you practice breaking down problems, the more intuitive the process will become.

By breaking addition and subtraction problems into smaller parts, you simplify calculations and reduce the risk of errors. This method not only helps in managing complex numbers but also builds a deeper understanding of arithmetic operations. Embrace this approach, and you’ll find that solving math problems becomes a more manageable and rewarding experience.