A block of mass 10 kg is kept on a rough inclined as shown in figure. The coefficient of friction between the block and the surface is 0.6 ...

A block of mass 10 kg is kept on a rough inclined ash shown in figure. The coefficient of friction between the block and the surface is 0.6. Two forces of magnitudes 3N & P Newton are acting of the block as shown figure. If friction on the block is acting upwards then minimum value of P for which the block remains at rest is:

Understanding Concepts:

Inclined planes are common scenarios in physics problems, where we analyze the effects of forces, friction, and gravity. This problem explores how to determine the minimum force required to keep a block stationary on a rough inclined surface. This concept not only tests understanding of Newton's laws but also provides insights into the role of friction.

Understanding Friction and Its Role in Keeping the Block Stationary

Friction is a critical factor in problems involving inclined planes. It acts in the opposite direction of potential motion, ensuring that objects remain stationary or slide at a controlled rate. In this case, the coefficient of friction (𝜇=0.6) indicates the strength of the frictional force relative to the normal force. The rough surface creates sufficient resistance, allowing the block to remain stationary when properly balanced with external forces.

The frictional force (𝑓) depends on the normal force, which is determined by the component of the block’s weight perpendicular to the incline. As the incline angle (𝜃) increases, the normal force decreases, reducing friction's ability to counteract the parallel component of gravity. This makes 𝑃, the external force, increasingly important to maintain equilibrium.

In practical terms, understanding this balance helps engineers design systems like brakes on ramps or machinery on slopes. By analyzing the forces in this scenario, we also gain insights into energy conservation and stability.

When approaching such problems, always remember to resolve forces correctly, account for friction’s direction, and verify that the net force aligns with the equilibrium condition. With this structured approach, you can solve even the most complex inclined plane problems effortlessly.

In this article, we’ll first break down the relevant concepts and then solve the given problem step-by-step.

Problem Statement

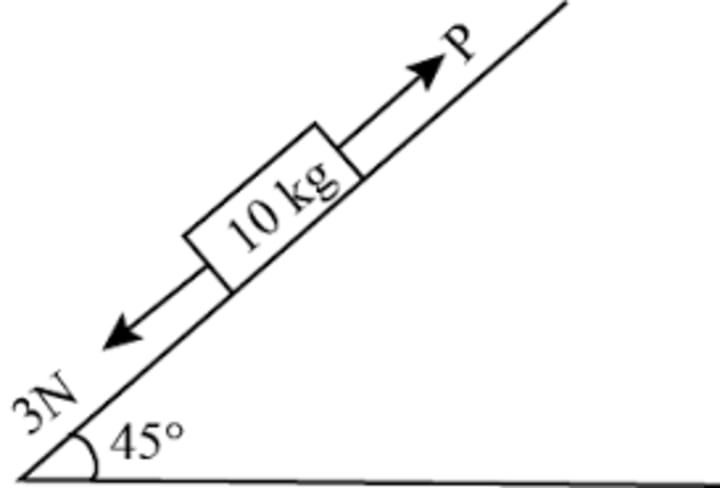
A block of mass m=10kg is kept on a rough inclined plane. The coefficient of friction (μ) between the block and the surface is 0.6. Two external forces, 3N and PN, act on the block. The frictional force acts upwards. Find the minimum value of P required to keep the block stationary.

Step-by-Step Solution

1. Given Values

Mass of the block: 𝑚= 10kg

Gravitational acceleration: 𝑔= 9.8m/s^2

Coefficient of friction: μ= 0.6

External force: 3N

Step 1: Components of Gravitational Force

The block’s weight:

W= mg= 10×9.8= 98N.

Resolve W into components:

- Parallel to the incline:

W parallel = 98sinθ.

- Perpendicular to the incline:

W⊥= 98cosθ.

Step 2: Normal Force and Frictional Force

The normal force is equal to the perpendicular component of the weight:

N= W⊥= 98cosθ.

The maximum static friction force: f= μN= 0.6×98cosθ= 58.8cosθ.

Step 3: Equilibrium Condition

For the block to remain stationary, the net force along the incline must be zero: P+f= W∥ + 3.

Substitute expressions for 𝑓 and W∥ : P+58.8cosθ= 98sinθ+3.

Solve for P: P= 98sinθ+3−58.8cosθ.

Step 4: Friction Direction Analysis

Since friction acts upwards, it opposes the motion caused by gravity and external forces. The positive contribution of friction reduces the required P.

Conclusion

The minimum force P required to keep the block stationary depends on the incline angle θ. If θ is provided, you can substitute its value into the equation:

P=98sinθ+3−58.8cosθ.

This calculation method is broadly applicable to similar physics problems involving inclined planes and friction.

If you liked this detailed explanation, let us know in the comments!

for More explanations you can visit:

BYJUS solution

Doubtnut solution

Testbook solution

Tardigrade solution