Quantum Consistency Condition and Closed Timelike Curves: An Examination of Deutsch’s Proposal

The possibility of closed timelike curves (CTCs) arises from the equations of general relativity. As a result of certain solutions, a particle may traverse a path that loops back to its past. One can observe that such phenomena bring about questions regarding causality and time. The means in which quantum mechanics addresses these issues is of considerable interest. This article examines the proposal put forward by David Deutsch, an Oxford physicist, who posited a self-consistency condition for particles on CTCs.

Deutsch’s proposal is built upon a core idea that the quantum state of a particle must remain unchanged after it travels through a closed timelike curve. It can be argued that this condition prevents the creation of paradoxes, such as a scenario in which a particle might interfere with the events leading to its own departure. The key element of this proposal is that the particle, when it returns to its past, must be in the same quantum state with which it left for the future. It can be posited that such a requirement provides a consistent framework within which quantum evolution is maintained. It is important at his juncture to note that this approach involves both the particle’s state and its interactions with external systems.

The means in which Deutsch formalises the self-consistency condition is by dividing the system into two parts: one that respects normal temporal order and one that follows the closed timelike curve. One can analyse this approach by considering a unitary operator, U, that acts to govern the interaction between the chronology-respecting (CR) subsystem and the CTC subsystem. The equation that characterises this interaction is given by

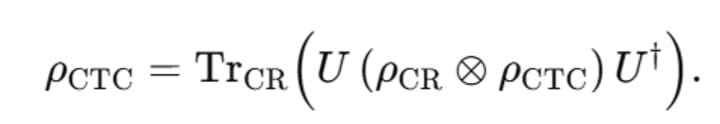
Thereupon, the equation indicates that the state of the CTC subsystem must remain as it was in the initial basis after the interaction, allowing for a fixed point solution. One could observe that this requirement, beneath the surface, acts to eliminate paradoxes by ensuring self-consistency. Owing to this formulation, the evolution of the quantum state exhibits non-linear characteristics. Ergo, the approach integrates quantum theory with time-travel scenarios in a manner that is both conceptually clear and mathematically robust.

Deutsch’s proposal introduces a notion that bridges quantum mechanics with non-standard causal structures. It can be argued that the self-consistency condition offers a mechanism by which paradoxes are avoided. One could argue that the concept of a fixed quantum state upon return acts to secure the causal loop from logical contradictions. One can observe that this framework is a primary example of how modifying the evolution of quantum states may lead to new computational possibilities. Owing to this ideology, researchers have speculated that exploiting such non-linear dynamics might potentially offer computational advantages over conventional quantum computers, within which the dynamics are governed by the principles of quantum mechanics. This idea is echoed in multiple theoretical studies.

One could argue that the proposal, notwithstanding this, faces challenges when applied to physical systems. One can analyse criticisms that the uniqueness of the fixed point is not guaranteed in every scenario and that multiple self-consistent solutions may be perceived. The means in which these ambiguities arise has been characterised by some as a potential drawback of the approach. It is important at his juncture to highlight that the physical realisation of closed timelike curves remains speculative. Owing to this, debates persist regarding the compatibility of non-linear evolution with established quantum principles. Ergo, the proposal offers a coherent solution to temporal paradoxes, and questions regarding its empirical foundation continue to come to the fore.

Deutsch’s consistency condition provides a framework in which quantum mechanics and closed timelike curves interact without giving rise to paradoxical scenarios. As such, the requirement that the quantum state remains invariant on its return is a primary, key element of the proposal. It can be argued that this condition, acting to secure causal integrity, opens new avenues for understanding time and computation. One could observe that beneath the surface, the ideas encapsulated in this approach challenge conventional interpretations of quantum evolution. The means in which the theory has been formalised offers insight into the interplay between quantum states and non-standard causal loops. This condition effectively prevents contradictions and secures the causal loop. This concept challenges traditional views on time and causality. Ergo, Deutsch’s work stands as a notion that continues to inspire further research within which the boundaries of physics may be expanded. As a result of the rigorous analysis, the scientific community has engaged deeply with the implications of such a framework.