Regular Expressions in Compiler Design

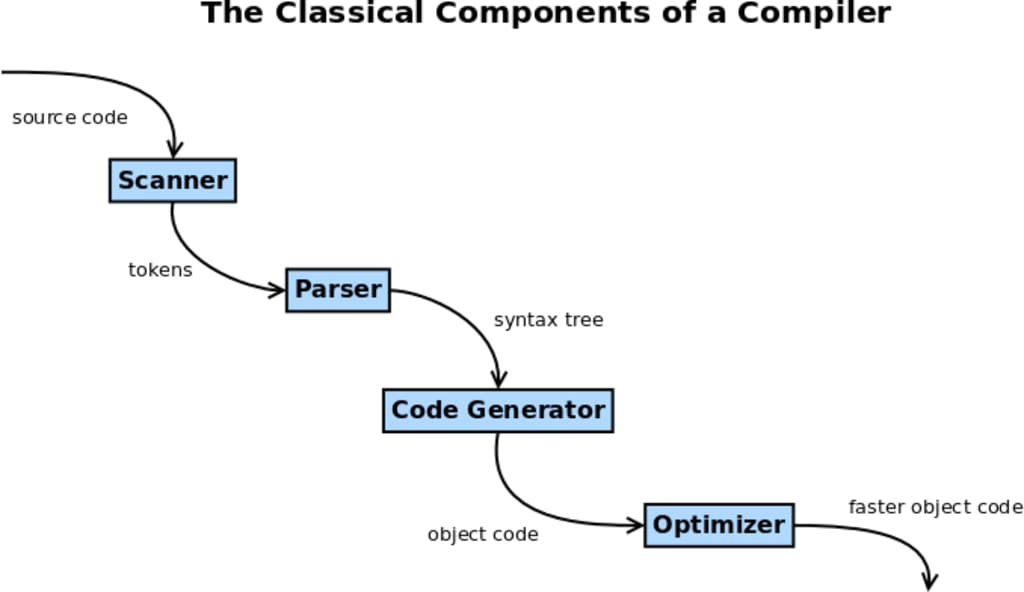
Regular expressions (regex) are a fundamental concept in compiler design, playing a crucial role in lexical analysis, the first phase of compiling source code into executable programs. They provide a powerful way to specify patterns for text processing and form the basis for token recognition in a compiler.

1. What Are Regular Expressions?

Regular expressions are sequences of characters that define a search pattern. They are used in pattern matching with strings, allowing for complex text manipulation and data validation. In compiler design, regular expressions are employed to specify patterns for tokens, which are the basic building blocks of programming languages.

A regular expression can describe patterns for strings using a combination of literals, operators, and special symbols. Here are some basic constructs:

Literals: Characters that match themselves (e.g., a, b, 1).

Concatenation: Sequences of expressions (e.g., ab matches a followed by b).

Union (Alternation): Choice between expressions (e.g., a|b matches a or b).

Kleene Star: Zero or more repetitions of an expression (e.g., a* matches a, aa, aaa, or the empty string).

Plus: One or more repetitions of an expression (e.g., a+ matches a, aa, aaa, but not the empty string).

Question Mark: Zero or one occurrence of an expression (e.g., a? matches a or the empty string).

Parentheses: Grouping expressions (e.g., (ab)* matches ab, abab, or the empty string).

2. Regular Languages and Finite Automata

Regular expressions define regular languages, which are a subset of formal languages recognized by finite automata. Finite automata are theoretical machines used to recognize patterns described by regular expressions. There are two main types of finite automata:

Deterministic Finite Automata (DFA):

A DFA has a single unique transition for each symbol in its alphabet from any given state. It consists of states, transitions, an initial state, and accepting states. DFAs are used for efficient pattern matching due to their predictable and non-ambiguous nature.

Nondeterministic Finite Automata (NFA):

An NFA can have multiple possible transitions for a given symbol, including epsilon transitions (transitions that occur without consuming an input symbol). NFAs are more flexible but can be converted into equivalent DFAs for practical implementation.

3. From Regular Expressions to Automata

The conversion process from regular expressions to finite automata involves several steps:

Regular Expression to NFA: Algorithms like Thompson's construction can convert a regular expression into an NFA. This involves creating states and transitions based on the operators in the regular expression.

NFA to DFA: The subset construction algorithm, also known as the powerset construction, is used to convert an NFA into a DFA. This process involves creating a DFA state for each possible subset of NFA states.

Minimization of DFA: Once a DFA is created, it can be minimized to reduce the number of states while preserving the language it recognizes. This optimization step is crucial for efficient lexical analysis.

4. Lexical Analysis and Tokenization

In compiler design, regular expressions are used to define the patterns for tokens, which are the smallest units of meaning in a programming language (e.g., keywords, identifiers, operators). The lexical analyzer, or lexer, uses regular expressions to identify tokens in the source code.

Here’s a high-level overview of how a lexer works with regular expressions:

Pattern Definition: Regular expressions are used to define patterns for various tokens (e.g., identifiers might be defined by [a-zA-Z_][a-zA-Z0-9_]*).

Token Recognition: The lexer reads the input source code character by character, matching substrings against the defined patterns.

Token Generation: When a pattern is matched, the lexer generates a token and continues processing the remaining input.

Error Handling: If the lexer encounters an input that doesn’t match any pattern, it reports a lexical error.

5. Practical Considerations

Efficiency: The conversion from regular expressions to finite automata and subsequent DFA minimization can impact the efficiency of the lexer. Optimizations and careful design can mitigate performance issues.

Flexibility: Regular expressions offer flexibility in defining patterns but can become complex for languages with intricate syntax. Tools and libraries (like Lex/Flex) automate much of the process.

Error Reporting: Lexers should provide meaningful error messages to help with debugging. Enhancing regex patterns with detailed error handling can improve developer experience.

6. Conclusion

Regular expressions are a foundational tool in compiler design, enabling the specification and recognition of tokens in programming languages. They bridge the gap between human-readable patterns and the formal mechanisms of finite automata used in lexical analysis. Understanding regular expressions and their role in finite automata provides insight into the internals of compiler design and contributes to more efficient and effective language processing.

By mastering regular expressions and their implementation, you’ll gain a deeper appreciation for how compilers work and how complex patterns can be systematically analyzed and processed.