Nobody has paid attention to the Pi formula for centuries.

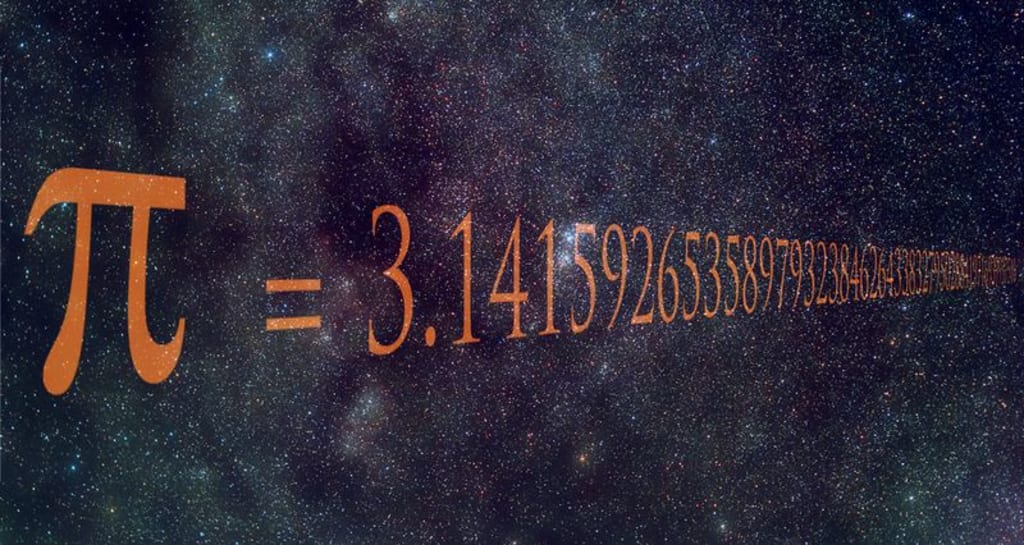
Which number is your favorite? There are countless possibilities, but only a select handful seems to be more popular than others: there are seven, of course; 13 or 666 for the badasses among us; and √2 for those who simply enjoy aggravating Pythagoreans.

However, pi is the only number that can legitimately stake a claim to being the world champion. What other mathematical constant serves as a benchmark for computing capability or is it the subject of a never-ending international competition to see who can correctly sort the most random numbers (current record: 111,700)?

Pi's ability to hold our attention in this way is a result of its irrationality or the fact that its decimal expansion is random and never-ending. It is believed that every possible sequence of integers may be found somewhere in the pi expansion, however knowing any particular sequence inside the expansion doesn't provide any clues as to which digit will follow next.

The following may seem virtually unbelievable in light of the fact that there has been a method for finding any certain pi digit since last year.

Of course, there's a catch: it relies on estimates to calculate the Euler and Bernoulli numbers, two sequences that can be laborious and time-consuming to calculate and that grow so quickly that it would be difficult to even fit them into your calculator, let alone successfully manipulate them to find the 14th digit of pi.

However, that isn't the exact purpose of the outcome: Simon Plouffe, a mathematician who secretly published his formula to the ArXiv preprint site in January 2022, claims that it is true and also elegant and straightforward. "It is a lovely formula, especially for base 2. Therefore, I believe we may conclude that the formula is really cool.

In fact, Plouffe has a bit of a thing for pi in base two: he's the P in the BBP algorithm, a technique for figuring out the nth digit of the binary expansion of pi that he first found back in 1995.

He claims that his outcome can now be applied to any base at all: "By adjusting for base 10 or base 2, it is valid for all n," the author says. If desired, it can be performed in any base; to do so, I can easily modify the formula.

Similar to the 1995 finding, the new formula is based on findings that "[were] known for centuries," according to him, but were infrequently revisited by practicing mathematicians.

Because of this, the new paper's most notable feature, aside from the result itself, is how brief it is—only six pages overall, not including a brief reference section.

Plouffe's conclusion doesn't require any complicated computations or abstract arguments; rather, it merely requires the capacity to view an old concept in a fresh way.

Because these Bernoulli numbers are so close to Pi and its powers, it seems plausible. "The equation that links them... I'd suppose that it must date back to Euler.

They are interconnected to the point that, if we isolate pi or pi to the nth power, we get a formula with the nth Bernoulli number, and it is so accurate that we can confirm that it is the nth decimal even if we truncate at the nth place.

It's unlikely that this discovery will have many practical applications, like so many others that have unlocked this most alluring of mathematical constants.

After all, even NASA's calculations with the highest accuracy, for tasks like interplanetary navigation, only call for expansions to about 16 significant figures. It's also difficult to envision a situation in which you would only need to be aware of one aspect of a number, such as the 143rd digit of pi.

But for mathematicians and pi enthusiasts alike, it's not so much about the application of the conclusion as it is about what it reminds us of: the notion that fascinating mathematical insights can be found anywhere if you just take a fresh look at things.

Why this outcome was overlooked for so long, "I confess that I don't know," but to see or find a property like that, you have to search with an eye that is looking for precisely that.