How does Linear Regression work? Implementation with sklearn.

Introduction

Hello viewers, I am Mustafa and in this blog, you are going to learn a simple Machine Learning algorithm called Linear Regression. We will go through some mathematics and then jump to the coding part. Trust me you require just a few lines to implement any model of machine learning, but the real thing you need to understand is how it works and the mathematics behind these Machine Learning algorithms. Let's get started!

So what is linear regression? what mathematical equations does it use to predict values?. I will try to answer these questions in this blog.

What is Regression?

Before moving on, let us understand what is regression?. Regression is a method used to predict future value or target value with the help of independent values or we can say features.

What is Linear Regression?

As the name suggests it is a linear model, so basically we can get good results if we have linear data. What is linear data? putting it simply, when we plot data we get a straight line with some angle (assuming it is 2-d data). So a regression model tries to fit the best possible line on training data with minimum loss.

The linear model makes predictions by simply computing the weighted sum of the input features, and a constant term called bias or intercept

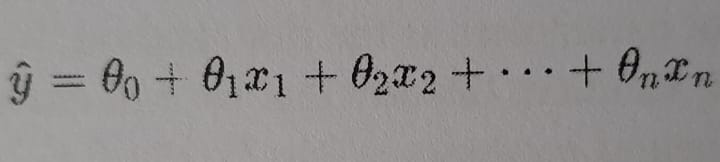
In this equation:

• y-hat is the predicted value.
• n is the number of features.
• x(i) is the ith feature value.
• θ is the model parameter or we can say feature weights.

How does a linear regression model train?

So that is the equation of the linear model, now how do we train it?. Traning a model means setting its parameter so that model best fits the training set. For this purpose, we first need a measure of how well the model fits the training data. So the most common performance measure for regression task is to apply Mean Square Error(MSE). To train the regression model we need to find a value theta that minimizes MSE.

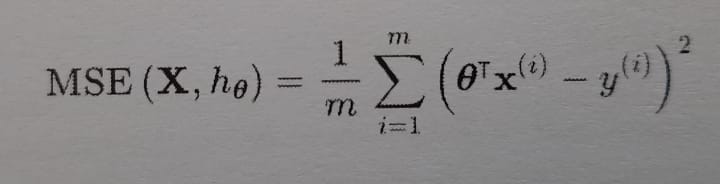
• X is a feature vector.
• h is the system's prediction function, also called a hypothesis.
• θ is the weight matrix.
• x(i) is an ith instance of X.
• y(i) is a target value of the ith instance.

To update the value of theta we will look at the basic equation first called Normal Equation.

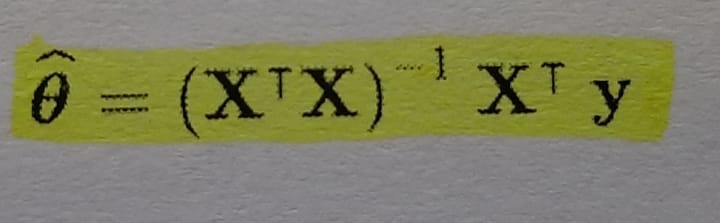
• θ is the value of θ that minimizes the cost function.
• y is the vector of target values containing y(1) to y(m).

Let's generate some data to test the above equation.

To generate data we have used numpy.random.rand() that gives us 100 size vector with some random values, and to generate our target value we have used 4x+3+(Some Gaussian noise). To implement the normal equation to get the best value of theta, We have used the numpy inv() function to calculate the inverse of matrix and dot() function to calculate dot product. Remember that equation that we used to generate data is 4+3x+(some Gaussian noise). We hoped to get values 4 and 3 but we got 4.215 and 2.7701 close enough.

Let's predict new values and plot them on a graph

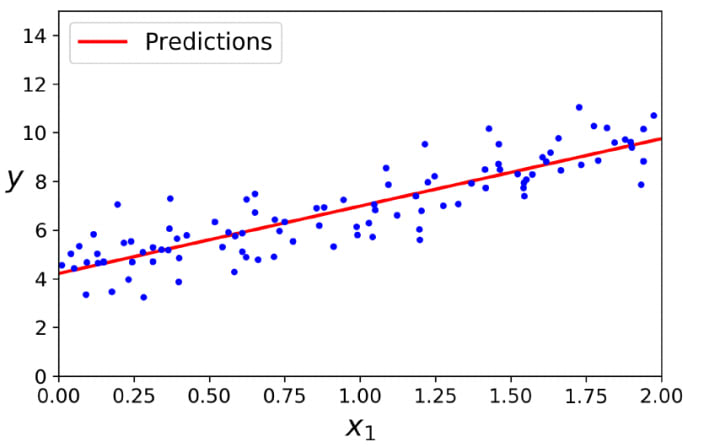
In the above code, we are generating 2 random values and passing them to predict method to get the target value. With help of the matplotlib library, we plot a scatter graph of training data and a line of data that we generated.

The LinearRegression class is based on the scipy.linalg.lstsq() function ( the name stands for "least squares"), which you could call directly:

This function computes θ = (X+) y, where X+ is the pseudoinverse of X. You can use np.linalg.pinv() to compute the pseudoinverse directly:

np.linalg.pinv(X_b).dot(y)

The pseudoinverse is computed as X+ = VΣ+UT(T is for transpose). V and U are orthogonal matrices.To compute the matrix Σ+, the algorithm takes Σ and sets to zero all values smaller than a tiny threshold value, then it replaces all the non-zero values with their inverse, and finally, it transposes the resulting matrix. But why use pseudo inverse instead of the normal equation? the Normal Equation may not work if the matrix XTX is not invertible (i.e., singular), such as if m < n or if some features are redundant, but the pseudoinverse is always defined.

Implementing Linear Regression using sklearn

Let's implement linear regression using the sklearn library.

So, quite an easy task to implement Linear Regression using sklearn. We just require 3 lines to implement it, firstly import the model from sklearn.linear_model, next initialize an object, and lastly call the fit method with feature values and target values as parameters.

Furthermore, you can evaluate the model and try GridSearchCV for hyperparameter tuning.

Please comment below if you find it useful or if you think some improvements are required. Thank you :)