Bresenham’s Line Drawing Algorithm in Computer Graphics

Introduction

In computer graphics, drawing a straight line on a pixel-based display can be a complex task. Lines are a fundamental component, and their accurate rendering is crucial for creating various shapes, wireframes, and graphical objects. Bresenham's Line Drawing Algorithm, developed by Jack E. Bresenham in 1962, offers an efficient and precise method for drawing lines on raster devices. This algorithm is celebrated for its simplicity, efficiency, and ability to operate using only integer arithmetic.

The Basics of Line Drawing

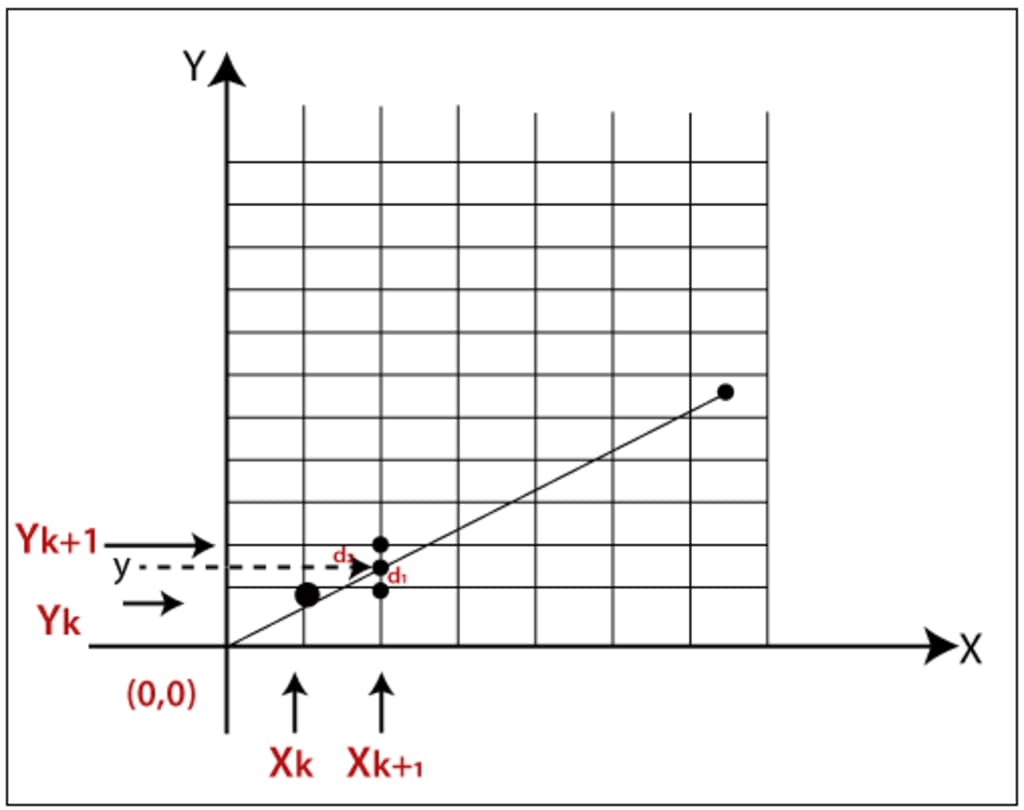
Before delving into Bresenham’s algorithm, it’s important to understand the problem it solves. When drawing a line between two points in a pixel grid, the challenge is to determine which pixels best approximate the ideal line. The line is defined by its two endpoints,

( 𝑥 0 , 𝑦 0 ) and ( 𝑥 1 , 𝑦 1 ).

The goal is to identify the pixels that closely follow the theoretical line equation:

𝑦 = 𝑚 𝑥 + 𝑐 where 𝑚 is the slope and 𝑐 is the y-intercept.

However, this equation often results in non-integer coordinates, which are not suitable for pixel grids.

Overview of Bresenham's Algorithm

Bresenham's Line Drawing Algorithm addresses this issue by using only integer calculations to determine the pixels that form the best approximation of a straight line. This makes the algorithm both fast and resource-efficient, suitable for real-time applications.

Key Concepts

Decision Parameter: The algorithm uses a decision parameter to determine whether the next pixel should be placed above or below the theoretical line.

Incremental Error: Instead of recalculating the slope at every step, Bresenham’s algorithm updates an error term incrementally.

Symmetry: The algorithm can handle all possible line slopes by considering symmetry and adjusting the algorithm accordingly for different octants.

Algorithm Steps

Initialization: Start with the initial point

( 𝑥 0 , 𝑦 0 ) . Calculate the differences Δ 𝑥 = 𝑥 1 − 𝑥 0 and Δ 𝑦 = 𝑦 1 − 𝑦 0 . Set the initial decision parameter 𝑝 = 2 Δ 𝑦 − Δ 𝑥.

Iterative Drawing: For each x-coordinate from 𝑥 0 to 𝑥 1:

Plot the current point

( 𝑥 , 𝑦 )

If 𝑝 ≥ 0 , increment 𝑦 by 1 (or decrement if the line is steep) and update 𝑝 by subtracting 2 Δ 𝑥.

Increment

𝑥 by 1 and update 𝑝 by adding 2 Δ 𝑦.

Pseudocode

Below is the pseudocode for Bresenham’s algorithm:

function BresenhamLine(x0, y0, x1, y1)

dx = abs(x1 - x0)

dy = abs(y1 - y0)

sx = (x0 < x1) ? 1 : -1

sy = (y0 < y1) ? 1 : -1

err = dx - dy

while (true)

plot(x0, y0)

if (x0 == x1 and y0 == y1) break

e2 = 2 * err

if (e2 > -dy)

err = err - dy

x0 = x0 + sx

if (e2 < dx)

err = err + dx

y0 = y0 + sy

Handling Different Slopes

The algorithm is designed to handle all octants by adjusting the incremental steps based on the slope. For steep lines (where ∣ 𝑚 ∣ > 1 ), the roles of 𝑥 and y is swapped, effectively drawing the line in a vertical fashion.

Advantages of Bresenham’s Algorithm

• Efficiency: The algorithm uses only integer arithmetic, making it computationally efficient.
• Accuracy: It minimizes the error in pixel approximation, producing visually appealing lines.
• Simplicity: The straightforward logic of the algorithm makes it easy to implement and understand.

Applications

Bresenham’s algorithm is widely used in various applications within computer graphics:

• Rendering: Used in rendering engines to draw edges of polygons and other shapes.
• Game Development: Essential for creating grid-based games and in-game graphics.
• Computer-Aided Design (CAD): Utilized in CAD software for drawing and designing geometric shapes.
• Raster Graphics Editors: Employed in programs like MS Paint for drawing lines.

Conclusion

Bresenham's Line Drawing Algorithm remains a cornerstone in computer graphics due to its efficient and accurate approach to rendering lines. Its reliance on integer arithmetic and incremental updates makes it ideal for real-time applications and systems with limited computational resources. Understanding and implementing Bresenham’s algorithm is a fundamental skill for anyone involved in computer graphics, game development, and related fields.