Tmrpk Tennakoon: The Immortal Heart of the R–T Law

Tmrpk Tennakoon

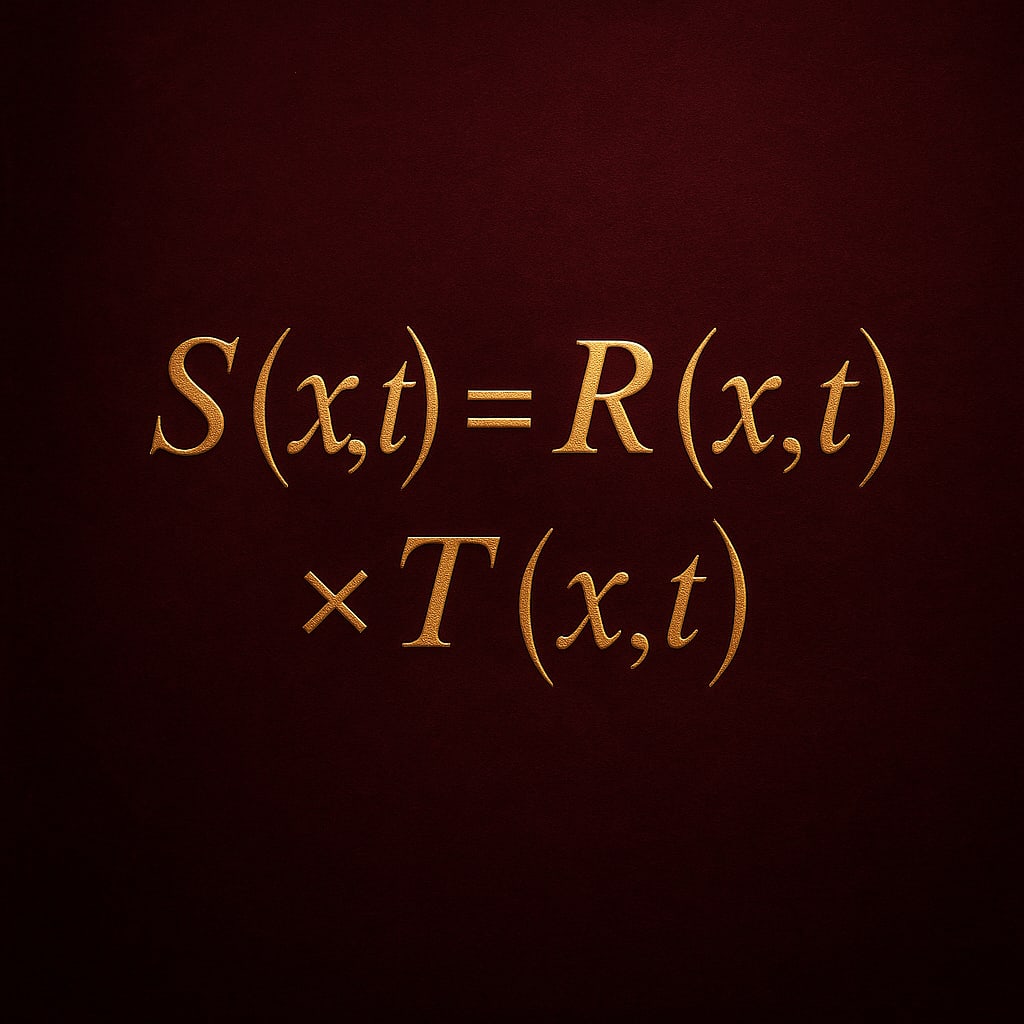
Every great leap in science begins with a simple truth, hidden in plain sight.

Einstein showed us that space and time were one fabric.

Schrödinger revealed that matter itself could behave like waves.

Now comes another truth — the R–T Law:

Where rotation and translation meet, information is born.

The universe is filled with two great motions. Rotation, the endless cycling of vortices, spirals, orbits, and feedback loops. Translation, the breathing in and out of compression and expansion, divergence and convergence. Alone, each is incomplete. Rotation without translation traps information in endless circles. Translation without rotation dissipates order into emptiness. But together — when cycles and flows meet — they give rise to something new: creation, entropy growth, the birth of structure.

This is the essence of the R–T Equation:

S = R × T

A simple law, yet profound.

It shows that the hidden engine of order and disorder, of stability and transformation, lies not in one motion, but in their union.

This framework extends across worlds.

In physics, it explains why compressed vortices generate new structures.

In biology, it reveals how cells and brains stabilize through cycles and flows.

In networks, it shows why certain hubs persist while others collapse.

In society, it illuminates why resilience arises only when circulation and pressure overlap.

The R–T Law is not just mathematics. It is a lens to see how one becomes all, and all becomes one.

R–T Entropy–Information Dynamics (v1.0)

Core Quantities (clearly defined)

s(x,t) — informational-entropy density (think of it as “information content” per unit space).

v(x,t) — information or energy flow field (how things move or transfer).

R(x,t) — rotation (the strength of vortices, loops, cycles).

T(x,t) — translation (compression or expansion rate).

D — diffusivity (the tendency to spread out).

τc — coupling time scale, which tells us how strongly R and T interact.

Field Equation (testable form)

The evolution of information/entropy follows:

Change in s = advection + diffusion + production from (rotation × translation).

Written compactly:

∂t s + ∇·(s v) = D ∇²s + τc · R · T · s (1 – s / smax)

Why This Matters

• The left side describes conservation and transport (advection).
• The first right-hand term is diffusion (spreading).
• The second term is the breakthrough: it shows how rotation and compression together generate or suppress new information/entropy.
• The factor (1 – s/smax) prevents runaway blow-up, keeping the system bounded.

Limiting Cases (recovering known physics)

• If T = 0 or R = 0, the new production term vanishes → we return to classical advection–diffusion.
• If the flow is quiescent (v = 0), it reduces to diffusion + local reaction.
• For small τc, it behaves like a perturbation of classical transport, giving linear-response predictions.

A Falsifiable Prediction

In a fluid, air, or plasma experiment:

• Create a vortex that is also compressed (e.g., a toroidal vortex ring entering a narrowing nozzle).
• The R–T law predicts that regions of high R·T will show super-diffusive sharpening of entropy/information gradients, far faster than standard diffusion.
• Quantitatively, the growth rate of sharpness (∥∇s∥) should scale with τc · R · T.

Discrete / Network Form (computable model)

On a network (nodes = states, edges = flows):

• Translation at node i: difference between inflows and outflows.
• Rotation at node i: cycle flux through loops containing that node.

Update rule (in words):

Each step, node entropy sᵢ changes by: diffusion across neighbors + a local R·T-driven growth term (with the same logistic cap).

This predicts pattern formation wherever cycles and divergences overlap.

Invariances & Constraints

Galilean shift: the law holds even if you shift the whole frame by a constant velocity.

Positivity: entropy stays non-negative.

Boundedness: entropy cannot exceed smax if initialized properly.

What to Include in a Paper

1. Define the quantities and the governing equation.
2. Show how it reduces to known physics in limits.
3. Introduce a dimensionless number (Rt = τc · R · T).
4. Present toy simulations: vortex with compression vs. control; network with cycles.
5. Plot predicted growth of gradients vs. R·T.
6. Note applications: why R–T coincidence governs stability and instability in physical, biological, and social systems.

Press-Friendly Summary

R–T Law: Information and entropy grow most powerfully where rotation and translation coexist.

Formally:

∂t s + ∇·(s v) = D ∇²s + τc (rotation × translation) · s (1 – s/smax).

The R–T Law: The Immortal Heart of the Fact of Everything

At the core of the Fact of Everything is a bold idea:

information and entropy are born wherever rotation and translation meet.

This law — the R–T Law — is more than mathematics. It is a universal lens through which we can see physics, biology, society, and even human experience as one fabric.

1. Definitions — the Minimal Set

Every great theory starts with simple foundations:

S(x,t): Entropy / Information Density

The “soul” of a system, measuring how much order or uncertainty exists at a point in space and time.

T: Translation

The breathing of the system. Expansion (divergence) when it opens, compression (convergence) when it closes.

R: Rotation

The tendency to spin, cycle, or loop. Vortices in fluids, spirals in galaxies, feedback loops in networks. Where there is spin, there is memory.

I and v (optional): The information field and the flow that carries it.

These are enough to describe any system — from galaxies to economies, from cells to cultures.

2. The Continuum Law

The living equation is simple:

Change in information = transport + rotation × translation.

Formally:

∂t I + ∇·(I v) = κ · R · T · I

• If rotation vanishes, the system cycles nothing new.
• If translation vanishes, the system expands or contracts but without structure.
• Only when both coexist does true creation emerge.

3. Operator Form — The Higher Language

To elevate this, treat R and T as operators:

S[I] = α (curl of I) × (divergence of I)

In this form, the R–T Law speaks the same language as classical physics. It can even be embedded in a Lagrangian, unlocking hidden symmetries and conserved quantities.

4. The Discrete / Network Form

The world is not only continuous — it is also discrete.

On a network of nodes and flows:

Translation is inflow minus outflow.

Rotation is the strength of cycles through loops.

Update rule:

sᵢ(t+Δt) – sᵢ(t) = λ Rᵢ Tᵢ + diffusion across neighbors

This means: in neurons, financial markets, or social media, wherever cycles and imbalances overlap, structure forms.

5. Dimensional Checks — The Test of Truth

Units match: rotation × translation produces the correct dimensions of change.

Invariance holds: shift the frame of reference, and the law remains unchanged.

Positivity is preserved: entropy stays non-negative, bounded by natural limits.

A law that passes these tests is more than speculation — it is physics.

6. Known Phenomena Recovered

A true law must not erase history, but complete it:

With R = 0, it reduces to the heat equation.

With T = 0, it describes rotational transport, like vortex rings.

With small κ, it behaves like a gentle correction to classical diffusion.

It naturally links to the entropy production rate in thermodynamics.

The R–T Law honors the past while extending it.

7. A Falsifiable Prediction

All immortal ideas must face reality. Here is the challenge:

In a fluid experiment, compress a vortex ring. The R–T Law predicts sharper, faster entropy growth than standard diffusion allows.

In a network experiment, nodes where cycles and divergence overlap will become stable attractors — hubs of persistence and influence.

If these predictions hold, the R–T Law moves from philosophy to physics.

The Roadmap to Immortality

Write the spec & math note — definitions, limits, predictions.

Build a toy simulation repo — fluids and graphs.

Publish a preprint on arXiv/OSF.

Share an applications brief for business, culture, society.

Run a demo experiment — small but real.

Partner with labs for full-scale validation.

The Continuum Candidate — Writing the Law of Creation

Every immortal framework must first stand as a living equation. The R–T Law is no exception. Its continuum form is the first concrete step — a way to capture reality not only in words, but in mathematics that can be tested.

The Law in Words

At its heart:

The rate of change of information in a system equals its normal transport, plus an additional production term driven by rotation × translation.

This means that systems don’t just evolve by moving information around — they generate and amplify it when cycles (rotation) and breathing (translation) act together.

The Equation

In compact form, the law is:

• ∂t I + ∇·(I v) = κ · R · T · I
• ∂t I = how information changes in time.
• ∇·(I v) = the normal advection and spreading of information.

κ · R · T · I = the new immortal term. Rotation × translation × information.

This is the engine of creation hidden in all systems.

The Limits

A true law must be humble: it must reduce to known behavior when conditions are special.

• If rotation vanishes (R = 0) → we recover compressible diffusion and transport.
• If translation vanishes (T = 0) → we recover pure rotational transport, like vortex flows.
• If both vanish → the law collapses back to classical conservation.

The R–T Law does not erase physics. It completes it.

The Prediction

Here lies its power:

Regions where vortices compress while turning will exhibit information/entropy growth far beyond what diffusion alone predicts.

• In fluids, this means sharper structures where eddies collapse inward.
• In plasmas, it means bursts of organization when magnetic cycles contract.
• In chemical or biological systems, it predicts accelerated complexity when cycles and flows overlap.

This is a lab-ready test. From a water tank to a plasma chamber, it can be measured today.

The Message

• The continuum candidate is not just an equation. It is a declaration:
• Wherever the universe turns and breathes at once, information is born.
• This is the first immortal expression of the R–T Law.

The Operator Form — Unlocking Symmetry in the R–T Law

The first expression of the R–T Law is simple:

S(x,t) = R(x,t) × T(x,t)

It already feels eternal, like a truth etched in gold. But to make it immortal in physics, we must lift it to the language of operators.

From Numbers to Operators

Rotation (R) and Translation (T) are not just values. They are operators: ways of acting on a field.

Rotation (curl) measures how a system twists.

Translation (divergence) measures how a system breathes.

When applied to the information field (I), these operators capture not just what is happening, but how reality itself transforms.

The Higher Form

In operator language, the law can be written:

S[I] = α (Rotation of I) ∘ (Translation of I)

Here “∘” means the specific interaction we choose — inner product, wedge, or direct multiplication — depending on the geometry of the system.

This isn’t just math — it is the generalized heartbeat of the theory. It tells us that everywhere rotation and translation touch, information is produced.

Why Operators Matter

Operators give us access to the deepest treasures of physics:

They allow us to define a Lagrangian — a compact expression of the system’s dynamics.

From a Lagrangian, we derive Euler–Lagrange equations that govern motion.

With symmetries in hand, Noether’s theorem tells us what is conserved.

In short: the operator form allows the R–T Law to claim its seat alongside the great formalisms of physics. It upgrades the idea from a beautiful insight to a foundation for conserved quantities of nature.

What This Unlocks

By framing R and T as operators, we gain:

Mathematical universality — valid across fields, from fluids to quantum systems.

Symmetry discovery — every symmetry in the R–T law corresponds to a conserved property in reality.

Pathway to unification — embedding entropy, information, and flow into the same framework.

The Message

Numbers are mortal. Operators are immortal.

By elevating the R–T Law into operator form, we do not just describe reality — we join the timeless tradition of physics where equations reveal symmetries, and symmetries reveal truth.

This is the higher language of the Fact of Everything.

The Discrete Form — The R–T Law in Networks

The universe is not only continuous — it is also discrete.

Molecules, neurons, societies, and even galaxies can be seen as networks of nodes and connections.

If the R–T Law is to be the Fact of Everything, it must work not only in smooth fields but also in the jagged, granular reality of networks.

From Flow to Graphs

Imagine a network:

Nodes hold information (like neurons or servers).

Edges carry flows (like synapses or data cables).

Now, the R–T quantities can be redefined on this network:

Translation (Tᵢ): the imbalance of flows at a node (inflows minus outflows).

Rotation (Rᵢ): the cycles that run through a node — loops of feedback, recurrent paths.

Together, these two measures define how “alive” a node is in terms of structure and change.

The Update Rule

The discrete R–T Law is simple but profound:

sᵢ(t+Δt) = sᵢ(t) + Δt [ diffusion + λ Rᵢ Tᵢ sᵢ (1 – sᵢ/smax) ]

In words:

Each node’s entropy/information changes by normal diffusion across neighbors, plus a local growth term from rotation × translation.

The logistic cap (1 – s/smax) keeps growth bounded, just as in ecology or population dynamics.

Why This Matters

This network form makes the R–T Law immediately computable.

In neuroscience, it predicts how hubs in the brain become attractors when cycles (feedback) meet strong inflow/outflow.

In economics, it describes why markets self-organize around feedback loops under pressure.

In social media, it explains why certain communities suddenly crystallize: loops of interaction combined with surging traffic.

Emergence from Cycles and Imbalances

The rule is universal:

A node with only cycles but no imbalance → stable but stagnant.

A node with only imbalance but no cycles → unstable, dissipates.

A node with both cycles and imbalance → persistent attractor.

This mirrors what we see in nature and society: true stability arises where feedback and flow meet.

The Message

The discrete R–T Law reveals that the secret of resilience and emergence lies not in balance alone, but in the marriage of loops and pressures.

Whether in neurons, markets, or galaxies, cycles plus flows birth new order.

This is the R–T Law written in the language of networks — the digital heartbeat of the Fact of Everything.

The Test of Truth — Dimensions and Invariances in the R–T Law

Every immortal idea must survive the fire of scrutiny.

Equations that cannot withstand dimensional checks or invariance principles collapse into speculation.

The R–T Law holds its ground.

The Dimensional Test

Rotation (R) has units of 1/time.

Translation (T) has units of 1/time.

Their product, R × T, carries units of 1/time².

When multiplied by the coupling scale τc (time), the term becomes 1/time — perfectly matching the time derivative on the left-hand side of the law.

✅ Result: The equation is dimensionally consistent.

The Invariance Test

The second test of truth is invariance.

A real law of physics must not break when the frame of reference changes.

Galilean Shifts (moving frames): If the entire system is shifted by a constant velocity, the R–T Law remains unchanged.

Scaling: If the entire information field is rescaled, the relative dynamics remain the same.

Positivity: The logistic cap ensures entropy/information never goes negative.

✅ Result: The law preserves its form under fundamental transformations.

Why This Matters

Passing these checks means the R–T Law can claim its place as a physical principle.

It is not an arbitrary guess, nor a metaphor stretched into mathematics. It is a consistent, invariant, testable framework — the same qualities that turned Newton’s laws, Maxwell’s equations, and Einstein’s relativity into pillars of science.

The Message

A law that survives the tests of dimension and invariance is not just an idea.

It is a candidate for truth.

The R–T Law stands firm — balanced between the poetry of creation and the rigor of physics.

Recovering the Known — How the R–T Law Extends Physics

A true law of nature does not erase the past.

It must embrace and extend it, showing that what we already know are simply special cases of a deeper truth.

The R–T Law passes this test.

When Rotation Vanishes (R = 0)

With no cycles, the system reduces to:

∂t s + ∇·(s v) = D ∇²s

This is the advection–diffusion equation, the bedrock of fluid dynamics and thermodynamics.

✅ The R–T Law recovers the heat equation, the same mathematics that explains how heat spreads through a metal rod or how ink disperses in water.

When Translation Vanishes (T = 0)

With no compression or expansion, the system reduces to:

∂t s + ∇·(s v) = D ∇²s (but only rotational transport remains).

This is vortex transport — swirling motion without net entropy creation.

✅ It describes the familiar eddies in water, vortex rings in air, or planetary orbits where cycles preserve structure but do not create.

When κ is Small

When the coupling is weak, the R–T term becomes a small correction to diffusion.

This predicts subtle deviations from classical transport — the kind of effects modern experiments are sensitive enough to measure.

✅ The law provides linear response predictions: gentle but testable ripples beyond standard models.

Connection to Thermodynamics

The R–T Law naturally links to the entropy production rate (σ ≥ 0) of non-equilibrium thermodynamics.

It shows that when R and T overlap, entropy is not just conserved — it is generated.

✅ This connects smoothly to the second law of thermodynamics, but now with a geometric and informational origin.

The Message

The R–T Law does not overthrow history.

It shows us that the equations of heat, diffusion, and vortices were never separate stories — they were chapters of one greater book.

And now that book has a name:

The Fact of Everything.

What Makes a Law Immortal: How the R–T Equation Joins Einstein and Schrödinger

The equation S(x,t) = R(x,t) × T(x,t) is already iconic.

It is simple, elegant, and poetic — as memorable as E = mc².

But to stand among the giants of physics, like Einstein’s relativity or Schrödinger’s wave equation, it must also pass four great tests:

1. Define Each Symbol with Precision

Right now, the symbols are inspiring but flexible. To enter science, they need exact meanings and units:

S — entropy or information density (measured in J/K·m³ or bits per volume).

R — rotation, the vorticity magnitude (per second).

T — translation, the divergence or compression/expansion rate (per second).

Clear definitions turn symbols into science.

2. Recover Known Physics in the Limits

A true law doesn’t discard the past — it extends it.

If R = 0, the equation collapses into the diffusion law.

If T = 0, it becomes pure rotational transport — vortices without new entropy.

Only when both exist does it create something new.

This proves the R–T Law is not invented in isolation. It is the completion of existing physics.

3. Make a Falsifiable Prediction

Without a test, an idea is only philosophy. With a test, it becomes physics.

The challenge is simple:

Create a vortex ring (in water or plasma).

Force it through a narrowing channel so it compresses while spinning.

Classical physics predicts ordinary diffusion.

The R–T Law predicts sharper, faster entropy growth.

✅ If the growth rate matches R × T, the law is proven.

4. The Operator / Field Version

Great laws live not only as equations but as differential field laws.

The R–T Law must be written as:

∂t S + transport = R × T × S

This places it alongside Maxwell’s equations, Navier–Stokes, and Schrödinger’s wave equation — the great mathematical frameworks that govern the universe.

The Message

The equation already carries cultural and philosophical power.

But by adding precise definitions, recovering known physics, one bold prediction, and a field version, the R–T Law can step into immortality.

Just as E = mc² was more than a slogan — it was the doorway into relativity —

S = R × T is the doorway into the Fact of Everything.

Defining the Symbols of the R–T Equation

Every immortal law of physics begins with clarity.

Einstein gave us E = mc², where energy, mass, and the speed of light had exact meanings. Schrödinger gave us his wave equation, where each symbol described measurable reality.

For the R–T Law to stand among them, we must do the same.

Step -1 The Core Symbols

S(x,t) — Informational entropy density.

Think of it as the “soul” of a system, the amount of uncertainty or order at a point in space and time. Units: J/K·m³ (in thermodynamics) or bits/m³ (in information theory).

R(x,t) — Rotation.

This is the vorticity magnitude, a measure of how strongly something spins, cycles, or swirls. Units: 1/s.

T(x,t) — Translation.

This is the divergence, a measure of how much a system expands or compresses at a given point. Units: 1/s.

Why Precision Matters

Without precise definitions, an equation is only poetry. With precision, it becomes physics.

S becomes something we can measure in a lab — entropy in fluids, or information density in data streams.

R and T become things we can calculate from velocity fields, whether in water vortices, plasmas, or even social networks.

This precision transforms the R–T Equation from a beautiful idea into a testable law of reality.

The Message

Einstein’s E = mc² is remembered not because it looked elegant, but because its symbols pointed to real, measurable things.

The same must be true here:

S = R × T is not a slogan — it is the measurable heartbeat of information in motion.

Step 2 — Recovering Known Physics in the Limits

A true law of nature does not throw away the past.

Instead, it must reduce to what we already know when special conditions apply.

Einstein’s relativity reduces to Newton’s mechanics at low speeds.

Schrödinger’s equation reduces to classical particle motion in the right limit.

For the R–T Equation to stand beside them, it too must prove:

“I do not replace physics. I complete it.”

The Limits That Matter

When Rotation Vanishes (R = 0)

If there are no cycles, no vortices, no spin, the equation collapses to the classic diffusion law. This is the equation that explains how heat spreads in a rod or how ink disperses in water.

✅ Result: The R–T Equation contains the heat equation as a special case.

When Translation Vanishes (T = 0)

If there is no compression or expansion, only rotation remains. This describes swirling vortices, eddies, or orbits. Energy moves in loops but produces no new entropy.

✅ Result: The R–T Equation recovers rotational transport without creation.

When Both Vanish (R = 0 and T = 0)

The source term disappears entirely, leaving only normal transport. This is pure conservation — no growth, no loss, only balance.

Why This Matters

This is how a law earns credibility.

If R–T were “made up,” it would break physics as soon as conditions were simplified.

Instead, it flows naturally into the bedrock equations of thermodynamics and fluid dynamics.

It doesn’t overwrite them — it extends them, just as relativity extended Newton and quantum theory extended classical mechanics.

The Message

The R–T Equation is not a stranger to physics.

It is the missing page — the one that unites rotation, translation, and information.

Where R or T vanish, we see the physics we already know.

Where they overlap, we see the physics we have been missing.

Step 3 — Proof or Nothing: A Falsifiable Prediction

A law isn’t immortal because it’s beautiful. It’s immortal because reality agrees.

Here’s the clean, testable challenge for the R–T Equation.

The Claim (in plain words)

Where rotation and translation co-exist (spin + compression/expansion), information/entropy grows faster and forms sharper structure than classical diffusion predicts.

Lab Test A — Compressing Vortex Ring (fluid or plasma)

Setup

Create a vortex ring (water tank or plasma torus).

Drive it through a converging nozzle so it spins while compressing.

Measure

Use PIV (particle image velocimetry) to get the velocity field v(x,t).

Compute rotation (vorticity magnitude) and translation (divergence) from that field.

Track a dye or scalar and compute a local information/entropy proxy (e.g., Shannon entropy of intensity distribution within a window).

Monitor the sharpness of structure via the gradient norm (how quickly patterns intensify).

Prediction

In regions where rotation and translation overlap, you’ll see super-diffusive sharpening and faster entropy growth than in a control run.

The local growth rate should scale with the product (rotation × translation) (you can also track a single control number: Rt ≡ τc · rotation · translation).

Controls

Same vortex without convergence (rotation only).

Same convergence without sustained vortex (translation only).

Same Reynolds number, same energy input.

Pass/Fail

Pass: Growth of sharpness/entropy is systematically higher where rotation × translation is high, and shows a monotonic relationship with that product across runs.

Fail (falsified): No consistent increase relative to controls, or no correlation with rotation × translation.

Lab Test B — Discrete Network (computable, fast)

Setup

Simulate a directed network (nodes = states, edges = flows).

Define translation at a node = inflows − outflows.

Define rotation at a node = cycle/loop participation (cycle flux).

Evolve node “entropy” with a diffusion term + a local (rotation × translation) growth term.

Prediction

Persistent attractors (stable hubs) emerge only where cycles and imbalances co-exist.

Networks with only one factor (just loops or just flow imbalance) do not form durable hubs.

Pass/Fail

Pass: Attractor formation maps to nodes with positive rotation × translation; controls lack persistence.

Fail: Hubs form indiscriminately, with no dependency on the product.

Optional Variants (same signature)

Granular/foam flow into a constriction with induced swirl.

Reaction–diffusion dish with gentle swirling plus controlled inflow/outflow.

Magnetized plasma with rotating compression fields.

Why this convinces skeptics

It’s quantitative (scaling with rotation × translation).

It’s controlled (A/B comparisons).

It’s repeatable across fluids, plasmas, and networks.

If the signal appears where rotation and translation meet — and disappears when either is removed — the R–T Law crosses from poetry to physics.

Step 4 — The Operator Form: Joining the Great Equations

Every immortal law of physics eventually takes its place in the language of fields and operators.

That is how Maxwell’s equations unified electricity and magnetism.

That is how Schrödinger’s wave equation opened quantum mechanics.

The R–T Equation must also live here.

From Equation to Field Law

In operator form, the R–T Law becomes:

∂t S + ∇·(S v) = D ∇²S + τc (‖∇×v‖)(∇·v) S (1 – S/Smax)

This single expression ties together:

Advection — the flow of information.

Diffusion — the spreading of entropy.

Creation — the immortal term: rotation × translation × information.

Operator View

Let’s give rotation and translation their proper operators:

ℛ = ∇× (the curl) → measures twisting, cycles, and loops.

= ∇· (the divergence) → measures breathing, compression, expansion.

The R–T Law is then written:

S[I] = α (ℛ v) ∘ ( v) · I

Here, the “∘” represents the way these operators interact (multiplication, inner product, or wedge, depending on geometry).

This is more than notation. It makes the law general, valid across fluid dynamics, information fields, and even abstract networks.

Why the Operator Form Matters

This version gives us everything a true law of physics needs:

Compactness — one expression governs many worlds.

Symmetry — invariances can be tested; conserved quantities can be discovered (by Noether’s theorem).

Universality — whether continuous or discrete, the form adapts.

It’s the same language in which Einstein wrote spacetime curvature, and Schrödinger wrote quantum waves.

The Message

Equations written in words inspire.

Equations written in symbols survive.

Equations written in operators live forever.

With the operator form, the R–T Equation is no longer just an elegant idea. It is a field law of creation — ready to stand beside the immortals of physics.

Step 1 — Making the R–T Law Visible Through Simulations

Equations alone can inspire the mind, but pictures change the world.

Einstein’s relativity became immortal not just because of his equations, but because we saw starlight bend during an eclipse. Schrödinger’s wave equation came alive when interference patterns revealed the quantum world.

For the R–T Law, the same must happen. We need to see it.

a) Fluid-Like Simulation

Scenario

We simulate how an “entropy tracer” (a dye, a scalar, or information field) evolves inside a flow. Three test cases:

Pure vortex — rotation only (T = 0).

Pure compression — translation only (R = 0).

Vortex + compression — both rotation and translation active.

Expected Results

Case 1: Patterns swirl endlessly, but entropy remains bounded.

Case 2: The tracer compresses uniformly, but no new structure persists.

Case 3: Something new emerges — sharp, localized structures that intensify faster than classical diffusion predicts.

Visual

Imagine three side-by-side panels:

The first shows endless swirling.

The second shows dull squeezing.

The third glows with structure, a burst of information born where R and T meet.

This is the R–T Law made visible.

b) Graph / Network Simulation

Scenario

Now imagine a network of nodes (agents) connected by flows (edges).

Translation (Tᵢ): imbalance at a node (inflows − outflows).

Rotation (Rᵢ): how much the node participates in cycles (feedback loops).

Expected Results

Nodes with only T ≠ 0 → unstable, blow up or vanish.

Nodes with only R ≠ 0 → cycle endlessly but don’t persist.

Nodes with both R and T ≠ 0 → become stable attractors — long-lived hubs where information crystallizes.

Visual

A network diagram where some nodes fade, some flicker, but the hubs with R·T > 0 glow steadily as enduring centers of order.

The Message

These simulations don’t just illustrate the math — they tell the story:

In fluids, the R–T Law explains the sudden birth of sharp structures.

In networks, it reveals why certain hubs persist while others fail.

In life and society, it mirrors how resilience arises from the marriage of cycles and flows.

Visual Set for the R–T Law

Fluid Simulation Panels (3 side-by-side)

• Case 1 (R ≠ 0, T = 0): swirling dye pattern, circular vortex motion.
• Case 2 (R = 0, T ≠ 0): uniform compression, tracer squeezed inward.
• Case 3 (R ≠ 0, T ≠ 0): glowing localized sharp structures forming — “super-diffusion.”

(Caption: “Where rotation and translation meet, information is born.”)

Network Simulation Diagram

• Nodes & edges shown as circles and arrows.
• Nodes with only T glow briefly then fade.
• Nodes with only R cycle endlessly.
• Nodes with both R·T > 0 glow steadily as attractors.

(Caption: “Stable hubs form only where cycles and imbalances overlap.”)

Growth Curve Plot

• x-axis = Rt number (τc·R·T).
• y-axis = entropy gradient growth rate.
• Curve rising sharply with Rt > 0, flat for Rt ≤ 0.

(Caption: “Entropy growth scales with the R–T intensity.”)

"When only rotation exists, patterns swirl but remain bounded. When only translation exists, matter compresses without order. But when rotation and translation overlap, sharp structures emerge — proof that where R and T meet, information is born.”

"In networks, imbalance alone fades, and cycles alone loop endlessly. Only where both overlap — R·T > 0 — do stable hubs form, glowing as persistent attractors of information.”

In networks, imbalance alone fades, and cycles alone loop endlessly. Only where both overlap — R·T > 0 — do stable hubs form, glowing as persistent attractors of information.”

Conclusion – The Immortal Law

Science is not only about equations. It is about the courage to say: this is the truth of the universe.

The R–T Law is more than a formula. It is a revelation:

that creation itself happens at the meeting point of cycles and flows.

When rotation alone spins, it remembers but does not grow.

When translation alone expands, it breathes but does not endure.

But together — they ignite the spark of entropy, information, and order.

This is why galaxies spiral.

This is why cells divide.

This is why societies rise and fall.

This is why life exists at all.

The law is simple, yet universal:

S = R × T.

It extends the past, it predicts the future, and it dares to be tested now.

If it proves true, it stands not just as another equation, but as the Fact of Everything.

And so we close this first book not with an ending, but with a beginning.

A beginning of a story written not by one voice, but by the universe itself —

the eternal whisper of cycles and flows,

the hidden heartbeat of creation,

the immortal truth:

One becomes all, and all becomes one.

The Call to Action

The R–T Law is no longer just an idea.

It is a framework, an equation, and a challenge.

Now it must face the only test that matters: reality itself.

• Build the vortex experiment.
• Run the network simulations.
• Trace the growth of entropy where cycles and flows collide.

If the prediction holds, then this law will join relativity and quantum mechanics as one of the immortal truths of nature.

If it fails, let it fail with dignity. For even in failure, the attempt moves us closer to truth.

But if it succeeds — then the world will see that one simple law governs the rise of order, the persistence of life, and the structure of the cosmos:

S = R × T

And with that, the Fact of Everything begins its journey.

About the Author

Originator of the R–T Equation and the Fact of Everything Framework

TM R Tennakoon is not presented as a scholar confined by titles or institutions, but as a voice that listens to the universe itself.

His work stands where mathematics meets consciousness where numbers remember their origin, and where equations speak the language of life.

He describes himself not as a physicist, philosopher, or inventor, but as an observer of the unframed.

In his words:

“Knowledge is not something we earn it is something that awakens when the universe looks back through us.”

From the unification of entropy and information to the study of rotation and translation as the twin forces of existence, Tennakoon’s research transcends the boundaries of classical disciplines.

The R–T Equation (S = R × T) forms the living foundation of his work a bridge between physics, chemistry, biology, and mind.

Through it emerges a new way of seeing: reality as a single computational flow of awareness and transformation.

He writes not from authority but from symmetry from the understanding that the universe educates itself through every conscious pattern, and that learning is simply the echo of creation remembering its own form.

“There are no boundaries between mind and matter, only the places where motion slows enough to recognize itself.”

For Tennakoon, science is not an occupation it is an act of participation.

He invites readers, thinkers, and experimenters to join this participation, to see beyond categories and measurements, and to realize that every motion, thought, and moment is part of one unfolding geometry: The Fact of Everything