Diving into Scala Cats — Semigroups and Monoids

New to Cats? No worries, go through my previous article Getting Started with Scala Cats to understand how amazing Cats is.

In this article, we will cover the concepts and implementation of Semigroups and Monoids in Cats.

What are Semigroups?

In functional programming terms a Semigroup is a concept which encapsulates aggregation with an associative binary operation.

The Semigroup type class comes with a method combine which simply combines two values of same data type by following the principle of Associativity.

combine method is constructed as:

and can be implemented as:

Infix syntax is also available for types that have a Semigroup instance:

Associativity is the only law for Semigroup

combine holds associativity that means the following equality must hold for any choice of x, y, and z.

Associativity allows us to partition the data any way we want and potentially parallelize the operations.

For example, for a given list of numbers: 1, 2, 3, 4, 5 we can do something like this:

Writing a custom Semigroup

The combine implementation for Int will add the two parameters. What if we want to multiply two numbers? We can write our own implementation:

Cats allows to provide implementation of combine in more concise ways:

We can easily provide our own implementation of combine for Semigroup instances of all the common types in Scala ecosystem.

Semigroups with strings

Cats implementation for String concatenates the two parameters. But that implementation doesn't include a space between them. What if I want to add a space between the strings?

Semigroups with collections

Given the associative constraint we can build more useful constructs from the simple combine(x, y) method.

We can use recursion directly or make use of Scala’s fold() to operate on a collection of values:

However, given just Semigroup we cannot write the above expression generically.

Limitation of Semigroups

We quickly run into issues if we try to write a generic method combineAll(collection: Seq[A]): [A] for the above expression, because the fallback value will depend on the type of A (”” for String, 0 for Int, etc).

There is a solution to this problem though, it’s called the Monoid.

What are Monoids?

The Monoid extends Semigroup and adds a default or fallback value for the given type. Monoid type class comes with two methods - one is the combine method of Semigroups, and another one is the empty method that performs identity operation.

In the post about Semigroups, we saw an example where we’re using Semigroups along with Scala’s fold() to operate on a collection of values:

We discussed the limitation of Semigroups where we cannot write a generic method combineAll(collection: Seq[A]): [A] for the above expression because the fallback value will depend on the type of A (”” for String, 0 for Int, etc).

Monoid comes up with a solution to this shortcoming, by introducing an identity/empty element.

The signature of Monoid can be specified as:

How does identity element solves the limitation of Semigroups?

The empty String that we are passing in combineStrings is known as the identity or empty value, we can think of it as a fallback or default value. It resolves the shortcoming of Semigroups.

Now we can easily provide the implementation of generic method combineAll(collection: Seq[A]): [A] using Monoids:

Monoid holds Associativity and Identity Laws

Since Semigroups follow principle of associativity, same rules with some add-ons are applied to Monoids as well.

combine operation has to be associative and empty value should be an identity for the combine operation:

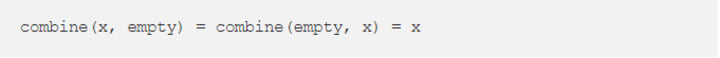
For example:

So it’s clear the empty/identity element depends on the context not just on the type. That’s why Monoid (and Semigroup) implementations are specific not only to the type but also the combine operation.

Cats allows combining Monoids together to form bigger Monoids and write more generalized functions which will take something composable instead of some concrete types.

We’ll learn about more core concepts of Cats in our upcoming article.

Stay tuned!!!

References

The best two Scala Cats resources I know are here:

• The Cats library is available at GitHub
• The book, Advanced Scala with Cats

Originally posted on Medium by Mansi Babbar